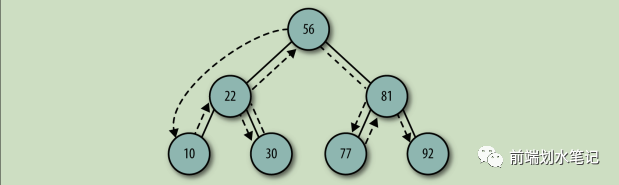
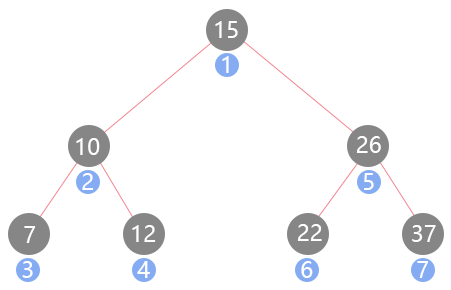
题目：输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1，2，4，7，3，5，6，8}和中序遍历序列{4，7，2，1，5，3，8，6}，则重建出图2.6所示的二叉树并输出它的头结点。

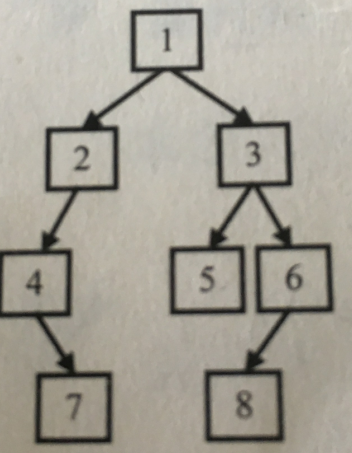
  思路：因为前序遍历先访问根结点，所以我们可以从前序遍历序列中先找到根结点1，然后中序遍历先访问左子结点，再访问根结点，最后访问右子结点。所以根结点1的左边为左子树结点，右边为右子树结点。以此类推，通过递归可重建该二叉树。

  测试用例:
  1.普通二叉树（完全二叉树，不完全二叉树）。
  2.特殊二叉树（所有结点都没有右子结点的二叉树，没有左子结点的二叉树，只有一个结点的二叉树）。
  3.特殊输入测试（二叉树的根结点指针为NULL，输入的前序遍历序列和中序遍历序列不匹配）。

#include<iostream>
#include<cstdio>
using namespace std;

struct BinaryTreeNode
{
    int                 m_nValue;
    BinaryTreeNode*     m_pLeft;
    BinaryTreeNode*     m_pRight;
};

BinaryTreeNode* ConstructCore(int* startPreorder, int* endPreorder,
                              int* startInorder, int* endInorder)
{
    //前序遍历序列的第一个数字是根结点的值
    int rootValue = startPreorder[0];
    BinaryTreeNode* root = new BinaryTreeNode();
    root->m_nValue = rootValue;  //将值赋给头结点
    root->m_pLeft = root->m_pRight = NULL; //把左右结点值设NULL

    if (startPreorder == endPreorder)  //前序遍历的头结点和尾结点相等，说明只有一个节点
    {
        if (startInorder == endInorder && *startPreorder == *startInorder)
        {
            return root;
        }
        else
        {
            throw exception("invalid input!");
        }
    }

    //在中序遍历中找到根结点的值
    int* rootInorder = startInorder;
    while (rootInorder <= endInorder && *rootInorder != rootValue)
    {
        ++rootInorder;
    }

    if (rootInorder == endInorder && *rootInorder != rootValue)
    {
        throw exception("invaild input!");
    }

    int leftLength = rootInorder - startInorder;
    int* leftPreorderEnd = startPreorder + leftLength;
    if (leftLength > 0)
    {
        //构建左子树
        root->m_pLeft = ConstructCore(startPreorder + 1, leftPreorderEnd,
                                       startInorder, rootInorder - 1);
    }

    if (leftLength < endPreorder - startPreorder)
    {
        // 构建右子树
        root->m_pRight = ConstructCore(leftPreorderEnd + 1,
                                       endPreorder, rootInorder + 1, endInorder);
    }

    return root;
}

BinaryTreeNode* Construct(int* preorder, int* inorder, int length)
{
    if (preorder == NULL) || inorder == NULL || length <= 0)
    {
        return NULL;
    }

    return ConstructCore(preorder, preorder + length - 1, inorder,
                         inorder + length - 1);

}