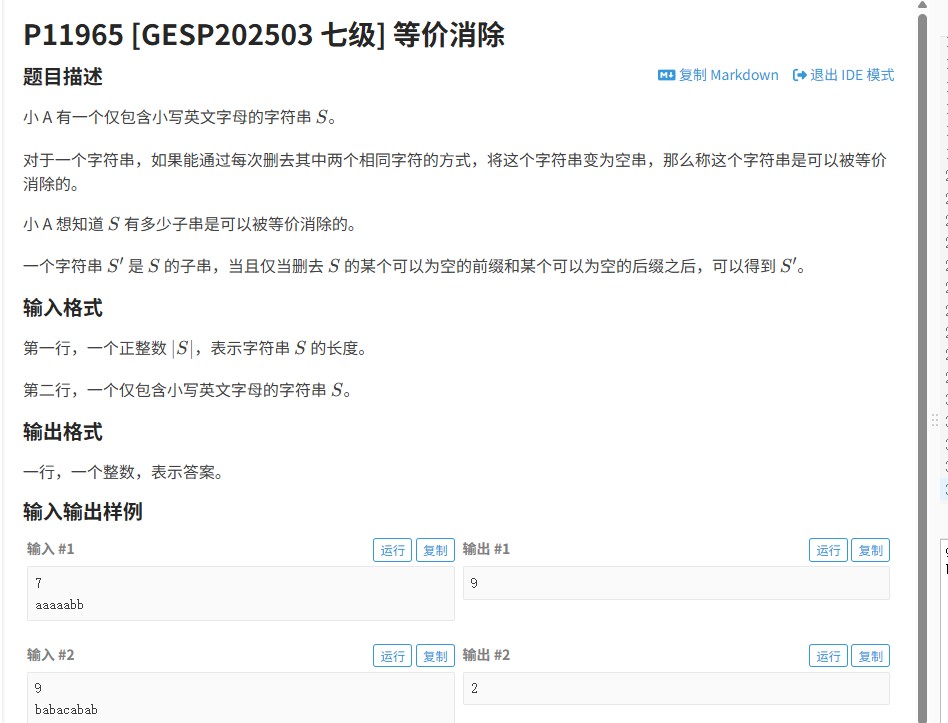
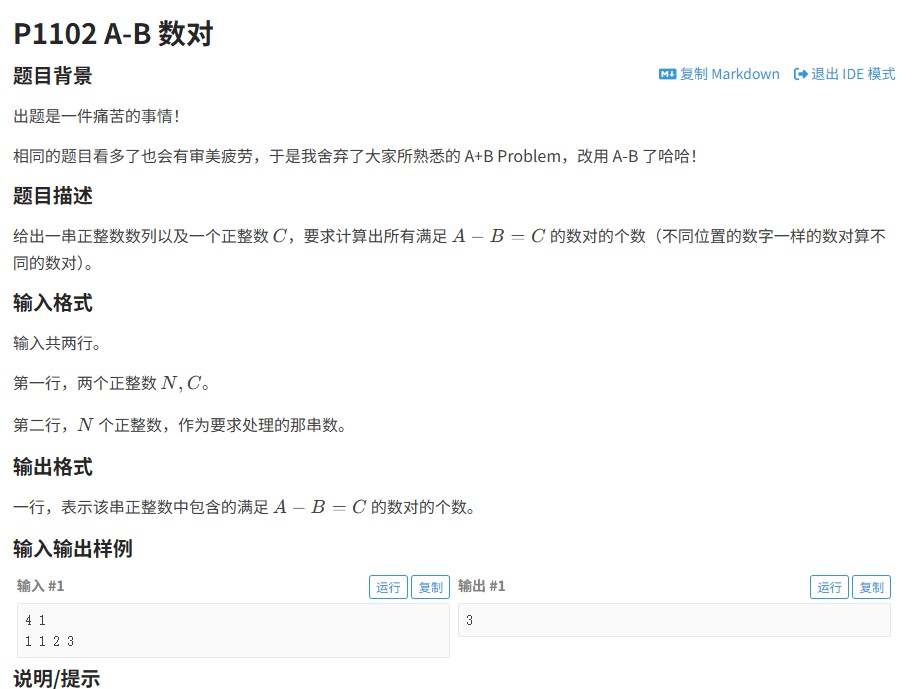
一、题目解读 本题为2012年NOIP提高组中的「借教室」问题（洛谷P1083），要求处理教室借用订单的分配问题。给定n天每天可用教室数量r和m个订单（订单包含需求教室数d、开始日期s、结束日期t），判断能否通过删除部分订单使所有订单满足教室容量限制。若能，输出需要删除的最少订单数；若所有订单必须保留，输出-1。题目核心在于将动态分配转化为判定性问题，通过二分查找优化求解。

二、解题思路 用户提供的代码采用二分查找解决。思路是将订单数作为二分范围，通过check函数判定是否存在可行解：

1. 转化为判定性问题：若删除前mid个订单能满足，则答案在[1, mid-1]中；否则在[mid+1, m]中。

2. 差分数组优化：用diff数组记录订单对每天教室数的增量（开始日+需求，结束日-需求），避免逐日模拟。

3. 边界处理与溢出防护：使用long long防止数据溢出，特判所有订单可满足的情况，避免二分循环。

三、解题步骤

1. 输入处理：读取n、m，教室容量r和订单信息d、s、t。

2. 二分查找框架：初始化left=1, right=m，答案ans初始化为m（最坏情况全删）。

3. 判定函数check(mid)：

   清空diff数组，遍历前mid个订单，按区间更新差分。

   计算每天累计需求current，若超过当日容量r，返回false。

4. 二分循环：根据check结果调整左右边界，最终ans为不可行的临界点。

5. 输出结果：特判全满足输出0，否则输出ans。

四、代码与注释

#include <iostream>
#include <vector>
#include <cstring>
using namespace std;

const int MAXN = 1e6 + 10;

int n, m;
int r[MAXN]; // 每天可用教室数
int d[MAXN], s[MAXN], t[MAXN]; // 订单信息
long long diff[MAXN]; // 使用long long防止溢出

bool check(int mid) {
    memset(diff, 0, sizeof(diff)); // 更安全初始化
    for (int i = 1; i <= mid; ++i) {
        diff[s[i]] += d[i];
        if (t[i] + 1 <= n) diff[t[i] + 1] -= d[i]; // 区间右端点差分
    }
    long long current = 0;
    for (int i = 1; i <= n; ++i) {
        current += diff[i];
        if (current > r[i]) return false; // 超容量即不可行
    }
    return true;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> r[i];
    for (int i = 1; i <= m; ++i) cin >> d[i] >> s[i] >> t[i];
    if (check(m)) { // 特判全满足
        cout << 0 << endl;
        return 0;
    }
    int left = 1, right = m, ans = m;
    while (left <= right) {
        int mid = (left + right) >> 1;
        if (!check(mid)) {
            ans = mid;
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    cout << -1 << endl << ans << endl;
    return 0;
}

五、总结 该代码通过二分查找将订单分配问题转化为判定性问题，结合差分数组高效处理区间影响，避免了O(nm)的暴力复杂度。关键点在于：

1. 利用二分查找缩小答案范围，降低时间复杂度至O(mlogm)。

2. 差分数组减少冗余计算，确保判定过程线性时间。

3. 特判与溢出防护提升代码鲁棒性。

此解法适用于区间修改与查询的判定场景，是竞赛中优化动态规划的经典技巧。

来源：2012年NOIP提高组：借教室题解