原文链接:http://tecdat.cn/?p=7227
神经网络的训练过程是一个挑战性的优化过程,通常无法收敛。
这可能意味着训练结束时的模型可能不是稳定的或表现最佳的权重集,无法用作最终模型。
解决此问题的一种方法是使用在训练运行结束时看到的多个模型的权重平均值。
平均模型权重
学习深度神经网络模型的权重需要解决高维非凸优化问题。
解决此优化问题的一个挑战是,有许多“ _好的_ ”解决方案,学习算法可能会反弹而无法稳定。
解决此问题的一种方法是在训练过程即将结束时合并所收集的权重。通常,这可以称为时间平均,并称为Polyak平均或Polyak-Ruppert平均,以该方法的原始开发者命名。
Polyak平均包括通过优化算法访问的参数空间将轨迹中的几个点平均在一起。
多类别分类问题
我们使用一个小的多类分类问题作为基础来证明模型权重集合。
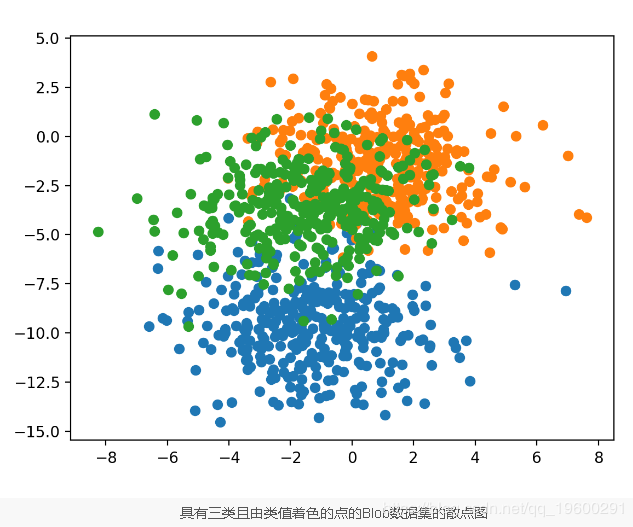
该问题有两个输入变量(代表点的_x_和_y_坐标),每组中点的标准偏差为2.0。
\# generate 2d classification dataset
X,y\=make\_blobs(n\_samples\=1000,centers\=3,n\_features\=2,cluster\_std\=2,random\_state\=2)
结果是我们可以建模的数据集的输入和输出元素。
为了了解问题的复杂性,我们可以在二维散点图上绘制每个点,并通过类值对每个点进行着色。
\# scatter plot of blobs dataset
\# generate 2d classification dataset
X,y\=make\_blobs(n\_samples\=1000,centers\=3,n\_features\=2,cluster\_std\=2,random\_state\=2)
\# scatter plot for each class value
forclass\_valueinrange(3):
\# select indices of points with the class label
row\_ix\=where(y\==class\_value)
\# scatter plot for points with a different color
pyplot.scatter(X[row\_ix,0],X[row\_ix,1])
\# show plot
pyplot.show()
运行示例将创建整个数据集的散点图。我们可以看到2.0的标准偏差意味着类不是线性可分离的(由线分隔),从而导致许多歧义点。
多层感知器模型
在定义模型之前,我们需要设计一个适合集合的问题。
在我们的问题中,训练数据集相对较小。具体来说,训练数据集中的示例与保持数据集的比例为10:1。这模仿了一种情况,在这种情况下,我们可能会有大量未标记的示例和少量带有标记的示例用于训练模型。
该问题是多类分类问题,我们 在输出层上使用softmax激活函数对其进行建模。这意味着该模型将预测一个具有三个元素的向量,并且该样本属于三个类别中的每个类别。因此,我们必须先对类值进行热编码,然后再将行拆分为训练和测试数据集。我们可以使用_Keras to\_categorical()_函数来做到这一点。
\# generate 2d classification dataset
X,y\=make\_blobs(n\_samples\=1100,centers\=3,n\_features\=2,cluster\_std\=2,random\_state\=2)
\# one hot encode output variable
y\=to\_categorical(y)
\# split into train and test
n\_train\=100
trainX,testX\=X[:n\_train,:],X[n\_train:,:]
trainy,testy\=y[:n\_train],y[n\_train:]
接下来,我们可以定义和编译模型。
该模型将期望具有两个输入变量的样本。然后,该模型具有一个包含25个节点的隐藏层和一个线性校正激活函数,然后是一个具有三个节点的输出层(用于预测三种类别中每个类别的概率)和一个softmax激活函数。
\# define model
model\=Sequential()
model.add(Dense(25,input\_dim\=2,activation\='relu'))
model.add(Dense(3,activation\='softmax'))
opt\=SGD(lr\=0.01,momentum\=0.9)
model.compile(loss\='categorical\_crossentropy',optimizer\=opt,metrics\=['accuracy'])
最后,我们将在训练和验证数据集上的每个训练时期绘制模型准确性的学习曲线。
\# learning curves of model accuracy
pyplot.plot(history.history['acc'],label\='train')
pyplot.plot(history.history['val\_acc'],label\='test')
pyplot.legend()
pyplot.show()
在这种情况下,我们可以看到该模型在训练数据集上达到了约86%的准确度 。
Train: 0.860, Test: 0.812
显示了在每个训练时期的训练和测试集上模型精度的学习曲线。

在每个训练时期的训练和测试数据集上模型精度的线图学习曲线
将多个模型保存到文件
模型权重集成的一种方法是在内存中保持模型权重的运行平均值。
另一种选择是第一步,是在训练过程中将模型权重保存到文件中,然后再组合保存的模型中的权重以生成最终模型。
\# fit model
n\_epochs,n\_save\_after\=500,490
foriinrange(n\_epochs):
\# fit model for a single epoch
model.fit(trainX,trainy,epochs\=1,verbose\=0)
\# check if we should save the model
ifi\>=n\_save\_after:
model.save('model\_'+str(i)+'.h5')
可以使用模型上的_save()_函数并指定包含纪元编号的文件名将模型保存到文件中。
pip install h5py
综合所有这些,下面列出了将模型拟合到训练数据集并保存最近10个时期中的所有模型的完整示例。
运行该示例会将10个模型保存到当前工作目录中。
具有平均模型权重的新模型
首先,我们需要将模型加载到内存中。
\# load models from file
defload\_all\_models(n\_start,n\_end):
all\_models\=list()
forepochinrange(n\_start,n\_end):
\# define filename for this ensemble
filename\='model\_'+str(epoch)+'.h5'
\# load model from file
model\=load\_model(filename)
\# add to list of members
all\_models.append(model)
print('>loaded %s'%filename)
returnall\_models
我们可以调用该函数来加载所有模型。
\# load models in order
members\=load\_all\_models(490,500)
print('Loaded %d models'%len(members))
加载后,我们可以使用模型权重的加权平均值创建一个新模型。
将这些元素捆绑在一起,我们可以加载10个模型并计算模型权重的平均加权平均值(算术平均值)。
首先运行示例将从文件中加载10个模型。
\>loaded model\_490.h5
\>loaded model\_491.h5
\>loaded model\_492.h5
\>loaded model\_493.h5
\>loaded model\_494.h5
\>loaded model\_495.h5
\>loaded model\_496.h5
\>loaded model\_497.h5
\>loaded model\_498.h5
\>loaded model\_499.h5
Loaded 10 models
从这10个模型中创建一个模型权重集合,为每个模型赋予相等的权重,并报告模型结构的摘要。
\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_
Layer (type) Output Shape Param #
\=================================================================
dense\_1 (Dense) (None, 25) 75
\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_
dense\_2 (Dense) (None, 3) 78
\=================================================================
Total params: 153
Trainable params: 153
Non-trainable params: 0
\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_
使用平均模型权重集合进行预测
既然我们知道如何计算模型权重的加权平均值,我们就可以使用生成的模型评估预测。
一个问题是,我们不知道要结合多少模型才能获得良好的性能。我们可以通过评估最近_n个_模型的模型权重平均合集来解决此问题,并改变_n_以查看有多少个模型产生良好的性能。
\# evaluate a specific number of members in an ensemble
defevaluate\_n\_members(members,n\_members,testX,testy):
\# reverse loaded models so we build the ensemble with the last models first
members\=list(reversed(members))
\# select a subset of members
subset\=members[:n\_members]
\# prepare an array of equal weights
weights\=[1.0/n\_membersforiinrange(1,n\_members+1)]
\# create a new model with the weighted average of all model weights
model\=model\_weight\_ensemble(subset,weights)
\# make predictions and evaluate accuracy
\_,test\_acc\=model.evaluate(testX,testy,verbose\=0)
returntest\_acc
\# reverse loaded models so we build the ensemble with the last models first
members\=list(reversed(members))
然后,我们可以评估从从最后1个模型到最后10个模型的训练运行中保存的最近_n个_模型的不同数量创建的模型。除了评估组合的最终模型外,我们还可以评估测试数据集上每个保存的独立模型以比较性能。
\# evaluate different numbers of ensembles on hold out set
single\_scores,ensemble\_scores\=list(),list()
foriinrange(1,len(members)+1):
\# evaluate model with i members
ensemble\_score\=evaluate\_n\_members(members,i,testX,testy)
\# evaluate the i'th model standalone
\_,single\_score\=members[i-1].evaluate(testX,testy,verbose\=0)
\# summarize this step
print('> %d: single=%.3f, ensemble=%.3f'%(i,single\_score,ensemble\_score))
ensemble\_scores.append(ensemble\_score)
single\_scores.append(single\_score)
可以绘制收集的分数,蓝色点表示单个保存的模型的准确性,橙色线表示组合了最后_n个_模型的权重的模型的测试准确性。
\# plot score vs number of ensemble members
x\_axis\=[iforiinrange(1,len(members)+1)]
pyplot.plot(x\_axis,single\_scores,marker\='o',linestyle\='None')
pyplot.plot(x\_axis,ensemble\_scores,marker\='o')
pyplot.show()
首先运行示例将加载10个保存的模型。
\>loaded model\_490.h5
\>loaded model\_491.h5
\>loaded model\_492.h5
\>loaded model\_493.h5
\>loaded model\_494.h5
\>loaded model\_495.h5
\>loaded model\_496.h5
\>loaded model\_497.h5
\>loaded model\_498.h5
\>loaded model\_499.h5
Loaded 10 models
报告每个单独保存的模型的性能以及整体模型的权重,该模型的权重是从所有模型(包括每个模型)开始平均计算的,并且从训练运行的末尾开始向后工作。
结果表明,最后两个模型的最佳测试精度约为81.4%。我们可以看到模型权重集合的测试准确性使性能达到平衡,并且表现也一样。
\> 1: single=0.814, ensemble=0.814
\> 2: single=0.814, ensemble=0.814
\> 3: single=0.811, ensemble=0.813
\> 4: single=0.805, ensemble=0.813
\> 5: single=0.807, ensemble=0.811
\> 6: single=0.805, ensemble=0.807
\> 7: single=0.802, ensemble=0.809
\> 8: single=0.805, ensemble=0.808
\> 9: single=0.805, ensemble=0.808
\> 10: single=0.810, ensemble=0.807
我们可以看到,对模型权重求平均值确实可以使最终模型的性能达到平衡,并且至少与运行的最终模型一样好。

线性和指数递减加权平均值
我们可以更新示例,并评估集合中模型权重的线性递减权重。
权重可以计算如下:
\# prepare an array of linearly decreasing weights
weights\=[i/n\_membersforiinrange(n\_members,0,-1)]
运行示例将再次报告每个模型的性能,这一次是每个平均模型权重集合的测试准确性,并且模型的贡献呈线性下降。
我们可以看到,至少在这种情况下,该集合的性能比任何独立模型都小,达到了约81.5%的精度。
...
\> 1: single=0.814, ensemble=0.814
\> 2: single=0.814, ensemble=0.815
\> 3: single=0.811, ensemble=0.814
\> 4: single=0.805, ensemble=0.813
\> 5: single=0.807, ensemble=0.813
\> 6: single=0.805, ensemble=0.813
\> 7: single=0.802, ensemble=0.811
\> 8: single=0.805, ensemble=0.810
\> 9: single=0.805, ensemble=0.809
\> 10: single=0.810, ensemble=0.809

具有线性衰减的单个模型测试性能(蓝点)和模型权重集合测试性能(橙色线)的线图
我们还可以对模型的贡献进行指数衰减的实验。这要求指定衰减率(α)。下面的示例为指数衰减创建权重,其下降率为2。
\# prepare an array of exponentially decreasing weights
alpha\=2.0
weights\=[exp(-i/alpha)foriinrange(1,n\_members+1)]
下面列出了模型对集合模型中平均权重的贡献呈指数衰减的完整示例。
运行该示例显示出性能的微小改进,就像在保存的模型的加权平均值中使用线性衰减一样。
\> 1: single=0.814, ensemble=0.814
\> 2: single=0.814, ensemble=0.815
\> 3: single=0.811, ensemble=0.814
\> 4: single=0.805, ensemble=0.814
\> 5: single=0.807, ensemble=0.813
\> 6: single=0.805, ensemble=0.813
\> 7: single=0.802, ensemble=0.813
\> 8: single=0.805, ensemble=0.813
\> 9: single=0.805, ensemble=0.813
\> 10: single=0.810, ensemble=0.813
测试准确性得分的线图显示了使用指数衰减而不是模型的线性或相等权重的较强稳定效果。















