需要考虑的问题
是否需要在二叉树的任意结点处插入子节点? (左右子树是否已满)
是否需要指定新数据元素(新节点)的插入位置?(左子树、右子树)
二叉树结点的位置枚举类型
enum BTNodePos
{
ANY,
LEFT,
RIGHT
};插入的方式
插入新结点
- bool insert(TreeNode<T> *node);
- bool insert(TreeNode<T> *node, BTNodePos pos);
插入数据元素
- bool insert(const T &value, TreeNode<T> *parent);
- bool insert(const T &value, TreeNode<T> *parent, BTNodePos pos);
新结点的插入

指定位置的结点插入
bool insert(n, np, pos)
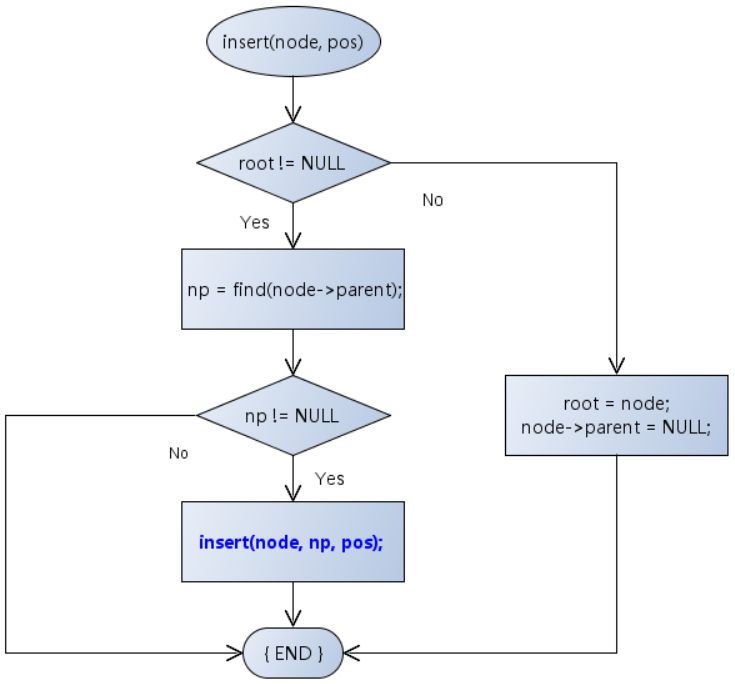
插入新结点
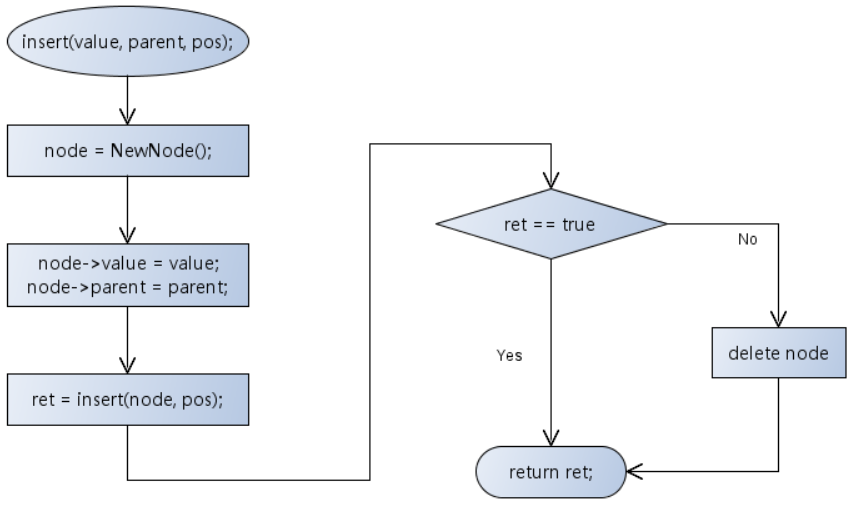
插入数据元素
编程实验:二叉树的插入操作
文件:BTree.h
#ifndef BTREE_H
#define BTREE_H
#include "Tree.h"
#include "BTreeNode.h"
#include "Exception.h"
#include "LinkQueue.h"
namespace DTLib
{
template <typename T>
class BTree : public Tree<T>
{
public:
BTree() = default;
bool insert(TreeNode<T> *node) override
{
return insert(node, ANY);
}
virtual bool insert(TreeNode<T> *node, BTNodePos pos)
{
bool ret = true;
if (node != nullptr)
{
if (this->m_root == nullptr)
{
node->parent = nullptr;
this->m_root = node;
}
else
{
BTreeNode<T> *np = find(node->parent);
if (np != nullptr)
{
ret = insert(dynamic_cast<BTreeNode<T>*>(node), np, pos);
}
else
{
THROW_EXCEPTION(InvalidParameterExcetion, "Invalid parent tree node ...");
}
}
}
else
{
THROW_EXCEPTION(InvalidParameterExcetion, "Parameter can not be null ...");
}
return ret;
}
bool insert(const T &value, TreeNode<T> *parent) override
{
return insert(value, parent, ANY);
}
virtual bool insert(const T &value, TreeNode<T> *parent, BTNodePos pos)
{
bool ret = true;
BTreeNode<T> *node = BTreeNode<T>::NewNode();
if (node != nullptr)
{
node->value = value;
node->parent = parent;
ret = insert(node, pos);
if (!ret)
{
delete node;
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No enough memory to create node ...");
}
return ret;
}
SharedPointer<Tree<T>> remove(const T &value) override
{
return nullptr;
}
SharedPointer<Tree<T>> remove(TreeNode<T> *node) override
{
return nullptr;
}
BTreeNode<T>* find(const T &value) const override
{
return find(root(), value);
}
BTreeNode<T>* find(TreeNode<T> *node) const override
{
return find(root(), dynamic_cast<BTreeNode<T>*>(node));
}
BTreeNode<T>* root() const override
{
return dynamic_cast<BTreeNode<T>*>(this->m_root);
}
int degree() const override
{
return 0;
}
int count() const override
{
return 0;
}
int height() const
{
return 0;
}
void clear() override
{
this->m_root = nullptr;
}
~BTree()
{
clear();
}
protected:
BTree(const BTree<T>&) = default;
BTree<T>& operator = (const BTree<T>&) = default;
virtual BTreeNode<T>* find(BTreeNode<T> *node, const T &value) const
{
BTreeNode<T> *ret = nullptr;
if (node != nullptr)
{
if (node->value == value)
{
ret = node;
}
else
{
if (ret == nullptr)
{
ret = find(node->left, value);
}
if (ret == nullptr)
{
ret = find(node->right, value);
}
}
}
return ret;
}
virtual BTreeNode<T>* find(BTreeNode<T> *node, BTreeNode<T> *obj) const
{
BTreeNode<T> *ret = nullptr;
if (node == obj)
{
ret = node;
}
else
{
if (node != nullptr)
{
if (ret == nullptr)
{
ret = find(node->left, obj);
}
if (ret == nullptr)
{
ret = find(node->right, obj);
}
}
}
return ret;
}
virtual bool insert(BTreeNode<T> *node, BTreeNode<T> *np, BTNodePos pos)
{
bool ret = true;
if (pos == ANY)
{
if (np->left == nullptr)
{
np->left = node;
}
else if (np->right == nullptr)
{
np->right = node;
}
else
{
ret = false;
}
}
else if (pos == LEFT)
{
if (np->left == nullptr)
{
np->left = node;
}
else
{
ret = false;
}
}
else if (pos == RIGHT)
{
if (np->right == nullptr)
{
np->right = node;
}
else
{
ret = false;
}
}
return ret;
}
};
}
#endif // BTREE_H文件:main.cpp
#include <iostream>
#include "BTreeNode.h"
#include "BTree.h"
using namespace std;
using namespace DTLib;
int main()
{
BTree<int> bt;
BTreeNode<int> *n = nullptr;
bt.insert(1, nullptr);
n = bt.find(1);
bt.insert(2, n);
bt.insert(3, n);
n = bt.find(2);
bt.insert(4, n);
bt.insert(5, n);
n = bt.find(4);
bt.insert(8, n);
bt.insert(9, n);
n = bt.find(5);
bt.insert(10, n);
n = bt.find(3);
bt.insert(6, n);
bt.insert(7, n);
n = bt.find(6);
bt.insert(11, n, LEFT);
int a[] = {8, 9, 10, 11, 7};
for (int i=0; i<5; ++i)
{
TreeNode<int> *node = bt.find(a[i]);
while (node)
{
cout << node->value << " ";
node = node->parent;
}
cout << endl;
}
return 0;
}输出:
8 4 2 1
9 4 2 1
10 5 2 1
11 6 3 1
7 3 1小结
- 二叉树的插入操作需要指明插入的位置
- 插入操作必须正确处理指向父结点的指针
- 插入数据元素时需要从堆空间中创建结点
- 当数据元素插入失败时,需要释放结点空间
To be continued
思考:如何实现 BTree (二叉树结构)的结点删除操作和清除操作
SharedPointer<Tree<T>> remove(const T &value) override
{
// ...
}
SharedPointer<Tree<T>> remove(TreeNode<T> *node) override
{
// ...
}
void clear() override
{
// ...
}以上内容整理于狄泰软件学院系列课程,请大家保护原创!