761. 特殊的二进制序列 : 经典构造题

题目描述

这是 LeetCode 上的 761. 特殊的二进制序列 ，难度为困难。

Tag : 「构造」

特殊的二进制序列是具有以下两个性质的二进制序列：

0 的数量与 1 的数量相等。
二进制序列的每一个前缀码中 1 的数量要大于等于 0 的数量。

给定一个特殊的二进制序列 S，以字符串形式表示。定义一个操作为首先选择 S 的两个连续且非空的特殊的子串，然后将它们交换。（两个子串为连续的当且仅当第一个子串的最后一个字符恰好为第二个子串的第一个字符的前一个字符。)

在任意次数的操作之后，交换后的字符串按照字典序排列的最大的结果是什么？

示例 1:

输入: S = "11011000"

输出: "11100100"

解释:
将子串 "10" （在S[1]出现） 和 "1100" （在S[3]出现）进行交换。
这是在进行若干次操作后按字典序排列最大的结果。

说明:

S 的长度不超过 $50$。
S 保证为一个满足上述定义的特殊的二进制序列。

构造

我们可以定义每个字符的得分：字符 1 得分为 $1$ 分，字符 0 得分为 $-1$ 分。

根据题目对「特殊字符串」的定义可知，给定字符串 s 的总得分为 $0$，且任意子串不会出现得分为负数的情况。

考虑将 s 进行划分为多个足够小特殊字符串 item（足够小的含义为每个 item 无法再进行划分），每个 item 的总得分为 $0$。根据 s 定义，必然可恰好划分为多个 item。

每次操作可以将相邻特殊字符串进行交换，于是问题转换为将 s 进行重排，求其重排后字典序最大的方案。

首先可以证明一个合法 item 必然满足 1...0 的形式，可通过「反证法」进行进行证明：定义了 item 总得分为 $0$，且长度不为 $0$，因此必然有 1 有 0。若第一位字符为 0，则必然能够从第一位字符作为起点，找到一个得分为负数的子串，这与 s 本身的定义冲突（s 中不存在得分为负数的子串）；若最后一位为 1，根据 item 总得分为 $0$，可知当前 item 去掉最后一位后得分为负，也与 s 本身定义冲突（s 中不存在得分为负数的子串）。

因此可将构造分两步进行：

对于每个 item 进行重排，使其调整为字典序最大
对于 item 之间的位置进行重排，使其整体字典序最大

由于题目没有规定重排后的性质，为第一步调整和第二步调整的保持相对独立，我们只能对 item 中的 1...0 中的非边缘部分进行调整（递归处理子串部分）。

假设所有 item 均被处理后，考虑如何进行重排能够使得最终方案字典序最大。

若有两个 item，分别为 a 和 b，我们可以根据拼接结果 ab 和 ba 的字典序大小来决定将谁放在前面。

这样根据「排序比较逻辑」需要证明在集合上具有「全序关系」:

我们使用符号 $@$ 来代指我们的「排序」逻辑：

如果 $a$ 必须排在 $b$ 的前面，我们记作 $a @ b$；
如果 $a$ 必须排在 $b$ 的后面，我们记作 $b @ a$；
如果 $a$ 既可以排在 $b$ 的前面，也可以排在 $b$ 的后面，我们记作 $a#b$；

2.1 完全性

具有完全性是指从集合 items 中任意取出两个元素 $a$ 和 $b$，必然满足 $a @ b$、$b @ a$ 和 $a#b$ 三者之一。

这点其实不需要额外证明，因为由 $a$ 和 $b$ 拼接的字符串 $ab$ 和 $ba$ 所在「字典序大小关系中」要么完全相等，要么具有明确的字典序大小关系，导致 $a$ 必须排在前面或者后面。

2.2 反对称性

具有反对称性是指由 $a@b$ 和 $b@a$ 能够推导出 $a#b$。

$a@b$ 说明字符串 $ab$ 的字典序大小数值要比字符串 $ba$ 字典序大小数值大。

$b@a$ 说明字符串 $ab$ 的字典序大小数值要比字符串 $ba$ 字典序大小数值小。

这样，基于「字典序本身满足全序关系」和「数学上的 $a \geqslant b$ 和 $a \leqslant b$ 可推导出 $a = b$」。

得证 $a@b$ 和 $b@a$ 能够推导出 $a#b$。

2.3 传递性

具有传递性是指由 $a@b$ 和 $b@c$ 能够推导出 $a@c$。

我们可以利用「两个等长的拼接字符串，字典序大小关系与数值大小关系一致」这一性质来证明，因为字符串 $ac$ 和 $ca$ 必然是等长的。

接下来，让我们从「自定义排序逻辑」出发，换个思路来证明 $a@c$：

761. 特殊的二进制序列 : 经典构造题

然后我们只需要证明在不同的 $i$ $j$ 关系之间（共三种情况），$a@c$ 恒成立即可：

当 $i == j$ 的时候：

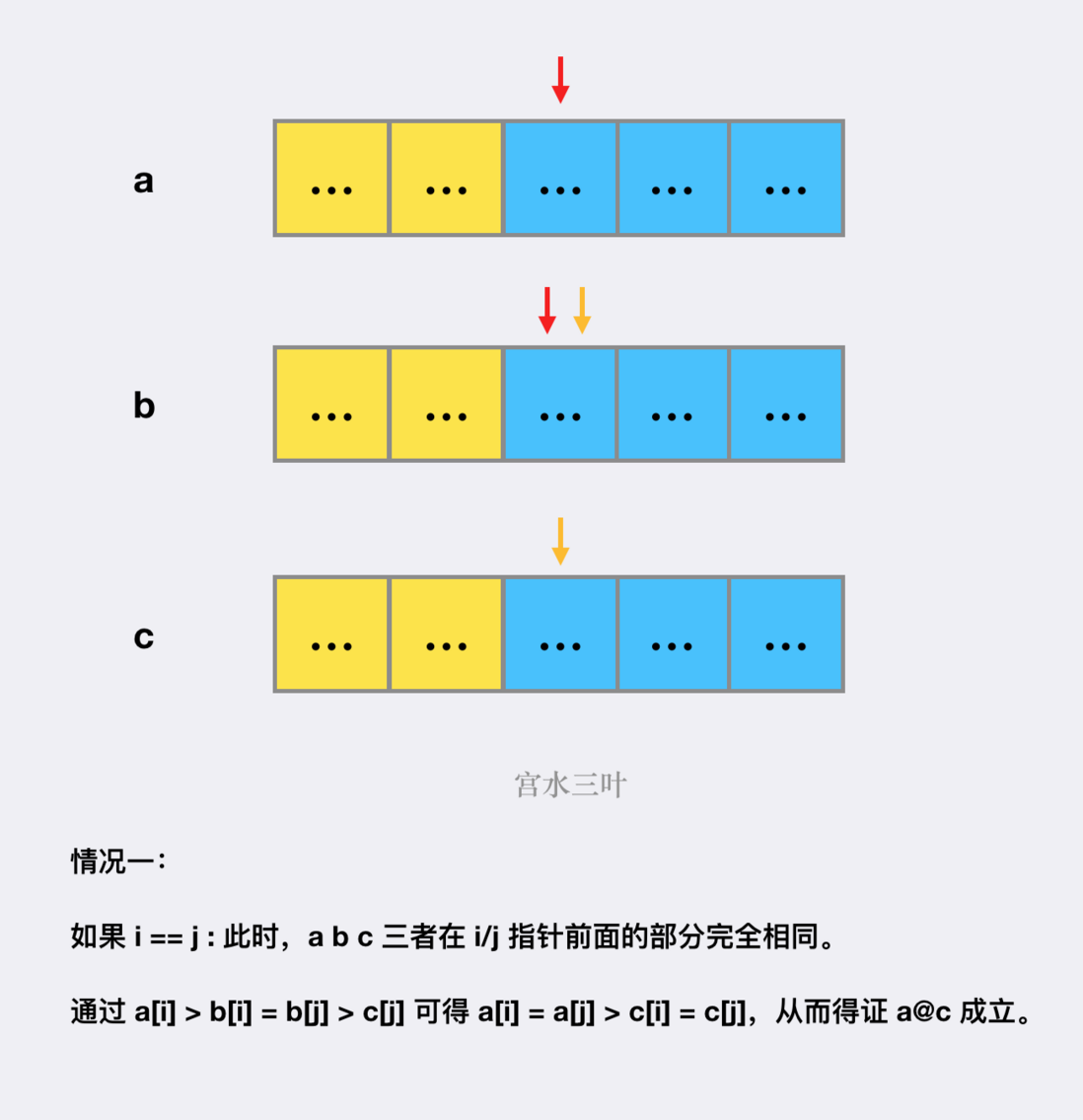
761. 特殊的二进制序列 : 经典构造题

当 $i > j$ 的时候：

761. 特殊的二进制序列 : 经典构造题

当 $i < j$ 的时候：

761. 特殊的二进制序列 : 经典构造题

综上，我们证明了无论在何种情况下，只要有 $a@b$ 和 $b@c$ 的话，那么 $a@c$ 恒成立。

我们之所以能这样证明「传递性」，本质是利用了自定义排序逻辑中「对于确定任意元素 $a$ 和 $b$ 之间的排序关系只依赖于 $a$ 和 $b$ 的第一个不同元素之间的大小关系」这一性质。

最终，我们证明了该「排序比较逻辑」必然能排序出字典序最大的方案。

Java 代码：

class Solution {
    public String makeLargestSpecial(String s) {
        if (s.length() == 0) return s;
        List<String> list = new ArrayList<>();
        char[] cs = s.toCharArray();
        for (int i = 0, j = 0, k = 0; i < cs.length; i++) {
            k += cs[i] == '1' ? 1 : -1;
            if (k == 0) {
                list.add("1" + makeLargestSpecial(s.substring(j + 1, i)) + "0");
                j = i + 1;
            }
        }
        Collections.sort(list, (a, b)->(b + a).compareTo(a + b));
        StringBuilder sb = new StringBuilder();
        for (String str : list) sb.append(str);
        return sb.toString();
    }
}

TypeScript 代码：

function makeLargestSpecial(s: string): string {
    const list = new Array<string>()
    for (let i = 0, j = 0, k = 0; i < s.length; i++) {
        k += s[i] == '1' ? 1 : -1
        if (k == 0) {
            list.push('1' + makeLargestSpecial(s.substring(j + 1, i)) + '0')
            j = i + 1
        }
    }
    list.sort((a, b)=>(b + a).localeCompare(a + b));
    return [...list].join("")
};