【系列推荐阅读】

1. 为什么要用到线索二叉树？

我们先来看看普通的二叉树有什么缺点。下面是一个普通二叉树（链式存储方式）：

线索二叉树的原理及创建

乍一看，会不会有一种违和感？整个结构一共有 7 个结点，总共 14 个指针域，其中却有 8 个指针域都是空的。对于一颗有 n 个结点的二叉树而言，总共会有 n+1 个空指针域，这个规律使用所有的二叉树。

这么多的空指针域是不是显得很浪费？我们学习数据结构和算法的重点就是在想法设法地提高时间效率和空间利用率。这么多的指针域就这么白白浪费了，太败家了！

所以我们要想法子好好利用它们，利用它们来帮助我们更好地使用二叉树这个数据结构。

那么如何利用呢？

前面已经强调过很多次了，遍历二叉树的实质是将二叉树中非线性结构的结点转化为线性的序列，然后才能方便我们遍历。

比如上图的中序遍历序列为：DBGEACF。

对于一个线性序列（线性表）来说，它有直接前驱和直接后继的概念（在【什么是线性表？】中介绍过）。比如在中序遍历序列中，B 的直接前驱为 D，直接后继为 G。

我们之所以能知道 B 的直接前驱和直接后继，是因为我们按照中序遍历的算法，把二叉树的中序遍历序列写出来了，然后根据这个顺序序列说谁的前驱是谁、后继是谁。

直接前驱和直接后继是不能完全直接通过二叉树得到的，因为二叉树中只有双亲和孩子结点之间的直接关系，即二叉树的结点指针域中只存储了其孩子结点的地址。

现在的需求是，我想能直接从二叉树上得到某结点在中序遍历方式下的直接前驱和直接后继。

这时候就需要用到线索二叉树了。

2. 什么是线索二叉树？

当然，我们肯定需要借助结点的指针域来保存直接前驱和直接后继的地址。

其实，在上图的普通二叉树中（以中序遍历得到的序列），部分结点（指针域不为空的结点）是可以找到其直接前驱或后继的，比如结点 E 的左孩子 G 就是结点 E 的直接前驱；结点 A 的右孩子 C 就是结点 A 的直接后继。

但部分结点（指针域为空）是行不通的，比如结点 G 的直接后继是 E，直接前驱是 B，但在二叉树中却不能得出这样的结论。怎么办呢？我们注意到，结点 G 的两个指针域都为 NULL，并未被利用，那么我们使用这两个指针，分别指向其前驱和后继不就好了吗？

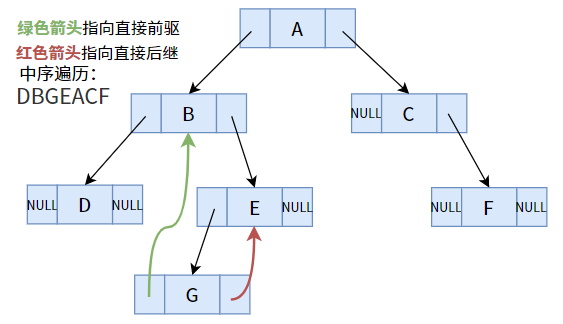
线索二叉树的原理及创建

实在是两全其美，天作之合！但是问题并没有解决！

因为我们是利用空指针域来指向前驱或后继的，对于那些指针域不为空的结点，这样是矛盾的，比如结点 E 和结点 B。

既然有矛盾，那么我们就发现产生矛盾的根源，解决矛盾。

产生矛盾的根源是：结点的指针域为空和不为空时，指针的指向矛盾。即，指针不为空时指向孩子和指针为空时指向前驱或后继之间的矛盾。

那么我们对症下药，把指针域为空和不为空给区分出来，清晰地告诉指针：不为空时指向孩子，为空时指向前驱或后继。这就需要我们给两个指针各添加一个标志位。

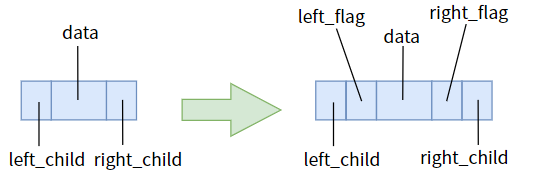
线索二叉树的原理及创建

并约定以下规则：

left_flag == 0 时，指针 left_child 指向左孩子
left_flag == 1 时，指针 left_child 指向直接前驱
right_flag == 0 时，指针 right_child 指向右孩子
right_flag == 1 时，指针 right_child 指向直接前驱

二叉树的结点要有所变化：

/*线索二叉树的结点的结构体*/
typedef struct Node {
    char data; //数据域
    struct Node *left_child; //左指针域
    int left_flag; //左指针标志位
    struct Node *right_child; //右指针域
    int right_flag; //右指针标志位
} TTreeNode;

有了标志位，一切就能理清了。我们称指向直接前驱和后继的指针为线索。标志位为 0 的指针是指向孩子的指针，标志位为 1 的指针是线索。

一个二叉链表树，结点结构如上，我们将所有空指针都变为线索，这样的二叉树就是二叉线索树。

3. 如何创造线索二叉树？

在普通二叉树中，我们想要获取某个结点在某种遍历次序下的直接前驱或后继，每次都需要遍历获取到遍历次序之后才能知道。而在线索二叉树中，我们只需要遍历一次（创造线索二叉树时的遍历），之后，线索二叉树就能“记住”每个结点的直接前驱和后继了，以后都不需要再通过遍历次序获取前驱或后继了。

我们按照某种遍历方式，把普通二叉树变为线索二叉树的过程被称为二叉树的线索化。

接下来，我们用中序遍历的方式，将下面的二叉树线索化为线索二叉树

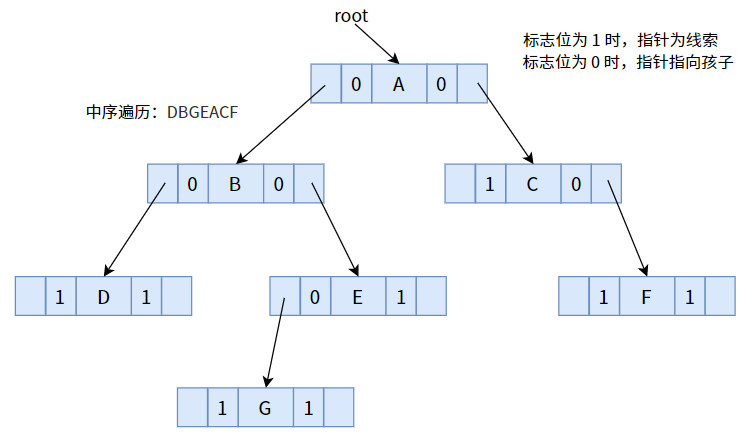
线索二叉树的原理及创建

将标志位为 1 的指针，按照中序遍历序列，使其指向前驱或后继：

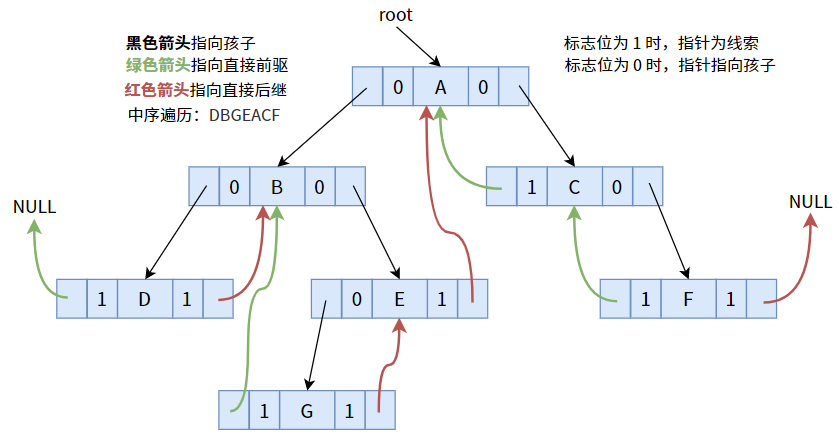
线索二叉树的原理及创建

其中，结点 D 没有直接前驱，结点 F 没有直接后继，故指针为 NULL。

到此，我们算是解决了拥有 n 个结点的二叉树存在 n+1 个空指针域所造成的浪费，解决方式是给每个结点的指针增加一个标志位，以此来利用空指针域。标志位中存储的是 0 或 1 的布尔值，与浪费的空指针域相比，是相对比较划算的。而且使二叉树具有了一种新特性——二叉树中能保存在某种遍历次序下的结点之间的前驱和后继关系。

4. 线索化的实现

请注意一点，线索二叉树是由普通二叉树得来的，而且是按某种遍历顺序得来的。因为线索是在知道某个结点的前驱和后继的情况下才能设置，而前驱和后继关系不能通过二叉树直接体现，只能通过遍历二叉树得到的线性序列得出关系。所以要通过某种遍历方式得到具有前驱和后继关系的序列后，才能修改结点的空指针，进而设置线索。

即：线索化的实质是在按照某种遍历次序进行遍历二叉树的过程中修改结点的空指针，使其指向其在该遍历次序下的直接前驱或直接后继的过程。

我们在【二叉树的遍历原理】和【二叉树的遍历实现】分别介绍了二叉树四种遍历方式的原理及代码实现。当时我们是以打印为例来介绍遍历的。但遍历不止做打印的事，还可以做线索化的事。

所以，代码的大体结构还是一样的，我们只需把遍历代码中的打印代码换成线索化的代码，并作出一些其他改变即可。

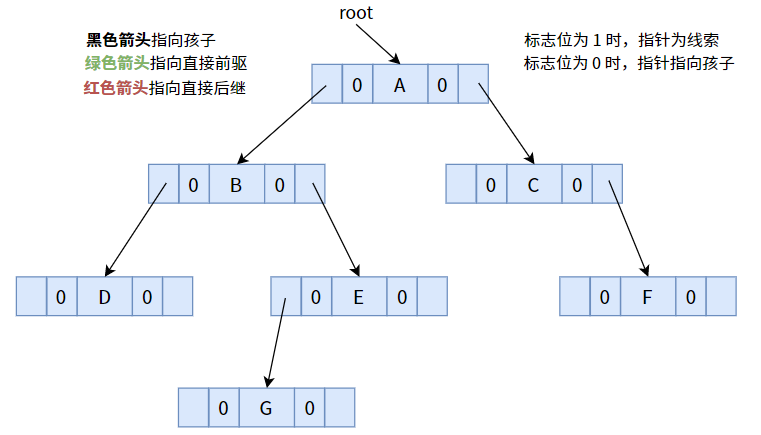
下面以下图为例，分别介绍三种线索化：

一颗未线索化的二叉树，其所有标志位均默认为 0.

线索二叉树的原理及创建

4.1. 中序线索化

按照中序遍历次序线索化后，可得下图：

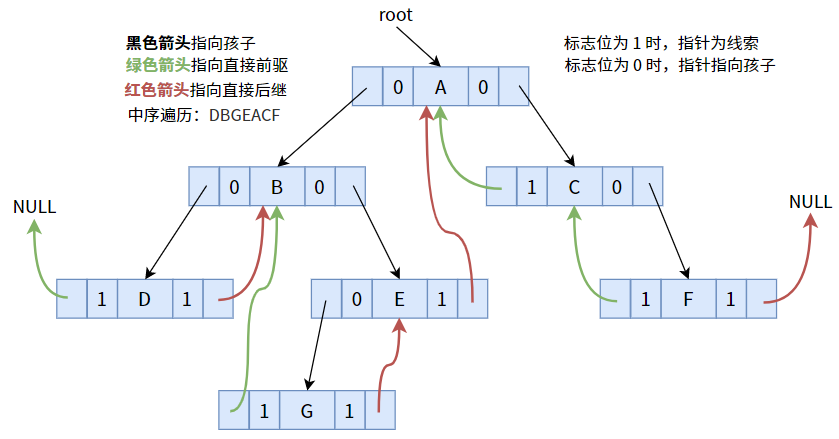
线索二叉树的原理及创建

我们先再次明确以下内容：

我们是在遍历二叉树的过程中进行线索化的。
中序遍历的顺序为：左子树 >> 根 >> 右子树。
线索化修改两个东西：空指针域和其对应的标志位。
如何修改？将空指针域置为直接前驱或后继。

所以我们的问题变成了：

找到所有空指针域。
找到空指针域所属结点，在先序次序下的直接前驱和直接后继。
修改空指针域的内容，及其标志位，使该指针称为线索。

说明：我们在遍历二叉树时，使用到了递归，所以在进行线索化的时候，也会使用它。

具体代码如下：

//全局变量 prev 指针，指向刚访问过的结点
TTreeNode *prev = NULL;

/**
 * 中序线索化
 */
void inorder_threading(TTreeNode *root)
{
    if (root == NULL) { //若二叉树为空，做空操作
        return;
    }
    inorder_threading(root->left_child);
    if (root->left_child == NULL) {
        root->left_flag = 1;
        root->left_child = prev;
    }
    if (prev != NULL && prev->right_child == NULL) {
        prev->right_flag = 1;
        prev->right_child = root;
    }
    prev = root;
    inorder_threading(root->right_child);
}

4.2. 先序线索化

按照先序顺序线索化后，可得下图：

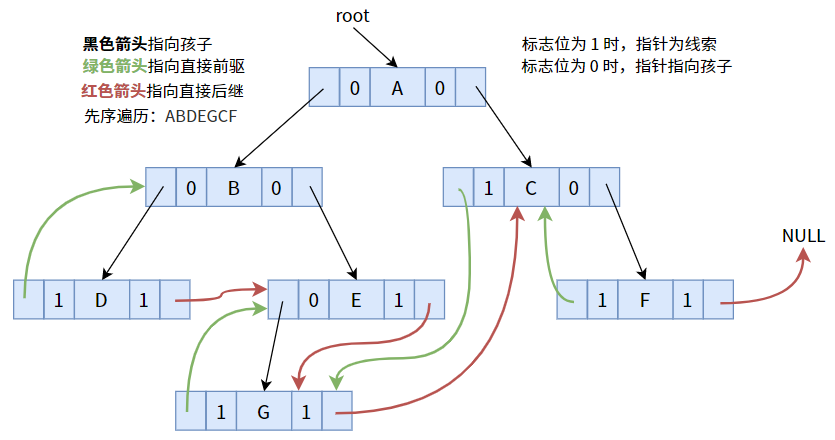
线索二叉树的原理及创建

具体代码如下：

// 全局变量 prev 指针，指向刚访问过的结点
TTreeNode *prev = NULL;

/**
 * 先序线索化
 */
void preorder_threading(TTreeNode *root)
{
    if (root == NULL) {
        return;
    }
    if (root->left_child == NULL) {
        root->left_flag = 1;
        root->left_child = prev;
    }
    if (prev != NULL && prev->right_child == NULL) {
        prev->right_flag = 1;
        prev->right_child = root;
    }
    prev = root;
    if (root->left_flag == 0) {
        preorder_threading(root->left_child);
    }
    if (root->right_flag == 0) {
        preorder_threading(root->right_child);
    }
}

4.3. 后序线索化

按照后序遍历次序线索化后，可得下图：

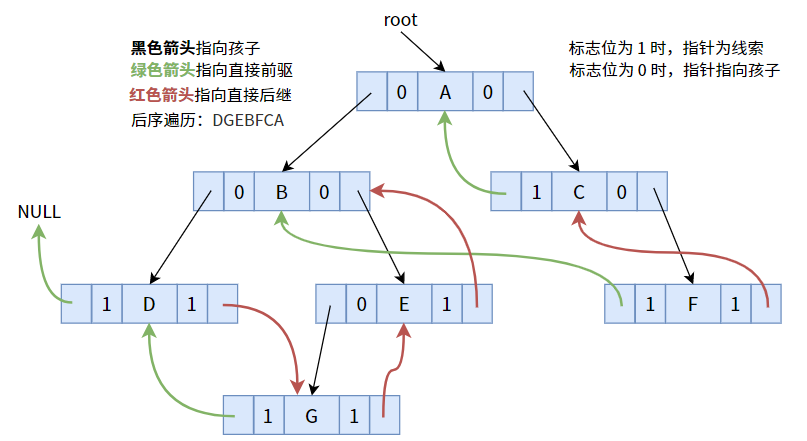
线索二叉树的原理及创建

具体代码如下：

//全局变量 prev 指针，指向刚访问过的结点
TTreeNode *prev = NULL;

/**
 * 后序线索化
 */
void postorder_threading(TTreeNode *root)
{
    if (root == NULL) {
        return;
    }
    postorder_threading(root->left_child);
    postorder_threading(root->right_child);
    if (root->left_child == NULL) {
        root->left_flag = 1;
        root->left_child = prev;
    }
    if (prev != NULL && prev->right_child == NULL) {
        prev->right_flag = 1;
        prev->right_child = root;
    }
    prev = root;
}