2024蓝桥杯省赛B组“传送阵”题解

一、题目解读

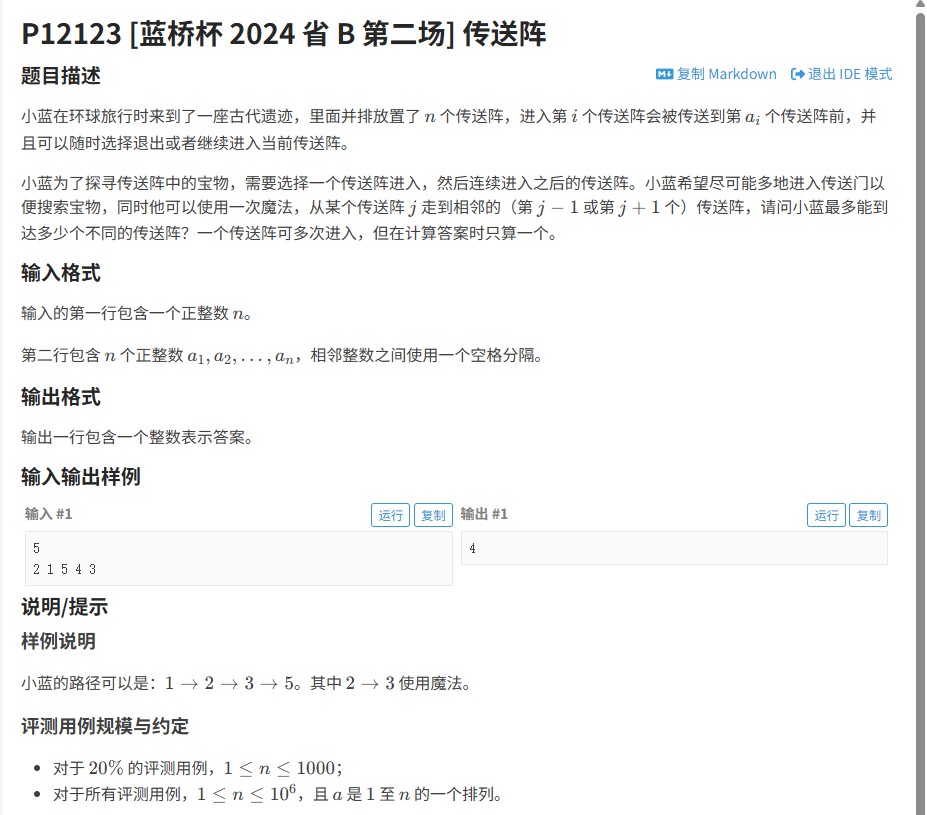
2024年蓝桥杯省B组“传送阵”题目要求处理一个包含n个节点的图，节点间存在单向传输关系。每个节点i可传送至a[i]指定的节点，形成可能存在的环结构。题目需求解从任意节点出发能到达的最长路径长度。本质上是图论中的最长路径问题，需考虑环的存在及节点间的连通性。

二、解题思路

预处理阶段使用标记法找出所有环，记录每个环的大小（即节点数）。
统计最大环和次大环尺寸。
计算基础结果：若存在次大环，结果为最大环+1；否则为最大环。
检查是否存在相邻节点属于不同环，若存在则合并两环得到更长的路径。

核心逻辑：利用环结构中的“循环路径”延长总路径，并通过节点间的连通性判断路径合并的可能性。

三、解题步骤

输入与初始化

读入节点数n及传输关系a[i]。

初始化辅助数组：cycle_id记录节点所属环编号，cycle_size存储各环尺寸。
环检测与尺寸统计

遍历节点，对未标记的节点i启动DFS：循环访问a[i]直至回到起点，标记路径上的节点并计数，形成环编号及尺寸。
计算基础结果

遍历cycle_size，更新最大环max1和次大环max2。

结果result初始化为max1+1（若max2存在）或max1。
路径合并判断

遍历相邻节点i和i+1，若所属环不同（cycle_id[i]!= cycle_id[i+1]），标记has_adjacent为true。

若存在相邻异环节点，更新结果result为max(max1+max2, result)。
输出最终结果。

四、代码与注释

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); // 优化输入输出速度

    int n;
    cin >> n;
    vector<int> a(n + 1); // 存储传输关系
    for (int i = 1; i <= n; ++i) cin >> a[i];

    vector<int> cycle_id(n + 1, 0); // 节点所属环编号
    vector<int> cycle_size; // 各环尺寸
    int id = 0; // 环编号计数器

    // 预处理：找出所有环
    for (int i = 1; i <= n; ++i) {
        if (cycle_id[i]) continue; // 已标记节点跳过
        id++; // 新环编号
        int cnt = 0, j = i; // 当前节点及计数
        while (!cycle_id[j]) { // 未标记的环路径
            cycle_id[j] = id; // 标记节点
            cnt++;
            j = a[j]; // 沿传输关系移动
        }
        cycle_size.push_back(cnt); // 记录环尺寸
    }

    // 统计最大环和次大环
    int max1 = 0, max2 = 0;
    for (int sz : cycle_size) {
        if (sz > max1) {
            max2 = max1;
            max1 = sz;
        } else if (sz > max2) {
            max2 = sz;
        }
    }

    // 基础结果：最大环+1（若存在次大环）
    int result = (max2 > 0)? max1 + 1 : max1;

    // 检查相邻节点是否在不同环
    bool has_adjacent = false;
    for (int i = 1; i < n; ++i) {
        if (cycle_id[i]!= cycle_id[i + 1]) { // 环编号不同
            has_adjacent = true;
            break;
        }
    }

    // 路径合并：若存在异环相邻节点，更新结果
    if (has_adjacent) {
        result = max(result, max1 + max2);
    }

    cout << result << endl;
    return 0;
}