十种基本排序算法

马邈
• 阅读 2324

概念

原地排序（Sorted in place） ：原地排序算法，就是特指空间复杂度是 ${O(1)}$的排序算法。
线性排序（Linear sort）：桶排序、基数排序、计数排序的时间复杂度是线性的，所以叫线性排序

性能比较

排序算法 平均时间复杂度 最好情况 最坏情况 空间复杂度 排序方式 稳定性
冒泡排序 ${O(n^2)}$ ${O(n)}$ ${O(n^2)}$ ${O(1)}$ In-place 稳定
插入排序 ${O(n^2)}$ ${O(n)}$ ${O(n^2)}$ ${O(1)}$ In-place 稳定
选择排序 ${O(n^2)}$ ${O(n^2)}$ ${O(n^2)}$ ${O(1)}$ In-place 不稳定
归并排序 ${O(nlogn)}$ ${O(nlogn)}$ ${O(nlogn)}$ ${O(n)}$ Out-place 稳定
快速排序 ${O(nlogn)}$ ${O(nlogn)}$ ${O(n^2)}$ ${O(logn)}$ In-place 不稳定
桶排序 ${O(n+k)}$ ${O(n+k)}$ 视情况而定 ${O(n+k)}$ Out-place 稳定
计数排序 ${O(n+k)}$ ${O(n+k)}$ ${O(n+k)}$ ${O(k)}$ Out-place 稳定
基数排序 ${O(n\times k)}$ ${O(n\times k)}$ ${O(n\times k)}$ ${O(n+k)}$ Out-place 稳定
堆排序 ${O(nlogn)}$ ${O(nlogn)}$ ${O(nlogn)}$ ${O(1)}$ In-place 不稳定
希尔排序 ${O(nlogn)}$ ${O(nlogn)}$ - ${O(1)}$ In-place 不稳定

1. 冒泡排序

1.1 最质朴的冒泡排序

按照冒泡排序的思路直接写出代码

public static void sort(int[] nums) {
    for (int i = 0; i < nums.length ; i++) {
        for (int j = 0; j < nums.length - 1 - i; j++) {
            if (nums[j] > nums[j + 1]) {
                swap(nums, j, j + 1);
            }
        }
    }
}

1.2 优化：sorted 标记+有序区间边界

public static void sort(int[] nums) {
    int border = nums.length-1;
    int lastChangeIndex = 0;
    boolean sorted = false;
    for (int i = 0; i < nums.length; i++) {
        sorted = true;
        for (int j = 0; j < border; j++) {
            if (nums[j] > nums[j + 1]) {
                sorted = false;
                swap(nums,j,j+1);
                // 保持一致性，j代表的是最后一次交换的左边位置，
                // 如果lastChangeIndex=j+1，就破坏了一致性
                lastChangeIndex = j;
            }
        }
        border = lastChangeIndex;
        if(sorted)return;
    }
}

1.3 鸡尾酒排序

鸡尾酒排序相当于双向的冒泡排序
当我们遇到一个序列，比如[2,3,4,5,6,7,8,9,1]，如果用单向的从左至右冒泡，则一直到最后一遍才会将1移动至合适的位置，而整个序列中，只有1一个数字是错位的，鸡尾酒排序主要解决的就是这种问题

public static void sort3(int[] nums) {
        boolean sorted = false;
        for (int i = 0; i < nums.length / 2; i++) {
            sorted = true;
            for (int j = i; j <nums.length-1-i ; j++) {
                if (nums[j] > nums[j + 1]) {
                    swap(nums, j, j + 1);
                    sorted = false;
                }
            }
            if(sorted)return;
            sorted = true;
            for (int j = nums.length-1-i; j >i ; j--) {
                if (nums[j] < nums[j - 1]) {
                    swap(nums, j, j - 1);
                    sorted = false;
                }
            }
            if(sorted)return;
        }
    }

2. 插入排序

2.1 代码实现

public static void sort(int[] array) {
    for (int i = 1; i < array.length; i++) {
        int key = array[i];
        int j = i-1;
        while (j >= 0 && array[j] > key) {
            array[j + 1] = array[j];
            j--;
        }
        array[j+1] = key;
    }
}

2.2 为什么虽然插入排序与冒泡排序复杂度相同，但是我们更喜欢用插入排序

冒泡排序不管怎么优化，元素交换的次数是一个固定值，是原始数据的逆序度。插入排序是同样的，不管怎么优化，元素移动的次数也等于原始数据的逆序度。但是，从代码实现上来看，冒泡排序的数据交换要比插入排序的数据移动要复杂，冒泡排序需要 3 个赋值操作，而插入排序只需要 1 个。
用我的机器做测试，数组大小为10W，结果对比很是很明显的

Bubblesort:22187ms
InsertSort:1154ms

3. 选择排序

public static void sort(int[] array) {
    for (int i = 0; i < array.length - 1; i++) {
        int min = i;
        for (int j = i; j < array.length; j++) {
            if (array[j] < array[min]) {
                min  = j;
            }
        }
        swap(array,i,min);
    }
}

4. 归并排序

/**
 * @Classname MergeSort
 * @Description 归并排序
 * @Date 2019/12/6 15:43
 * @Created by SunCheng
 */
public class MergeSort {
    public static void sort(int[] nums) {
        mergeSort(nums, 0, nums.length - 1);
    }

    private static void mergeSort(int[] nums, int l, int r) {
        if(l>=r)return;
        int mid = (l + r) >>> 1;
        mergeSort(nums, l, mid);
        mergeSort(nums, mid + 1, r);
        merge(nums, l, mid, r);
    }

    private static void merge(int[] nums, int l, int mid, int r) {
        int[] temp = new int[r - l + 1];
        int p1 = l,p2 = mid+1;
        int k = 0;
        while (p1 <= mid && p2 <= r) {
            if (nums[p1] <= nums[p2]) {
                temp[k++] = nums[p1++];
            } else {
                temp[k++] = nums[p2++];
            } 
        }
        while(p1<=mid) temp[k++] = nums[p1++];
        while(p2<=r) temp[k++] = nums[p2++];
        for (int i = 0; i < temp.length; i++) {
            nums[i+l] = temp[i];
        }
    }
}

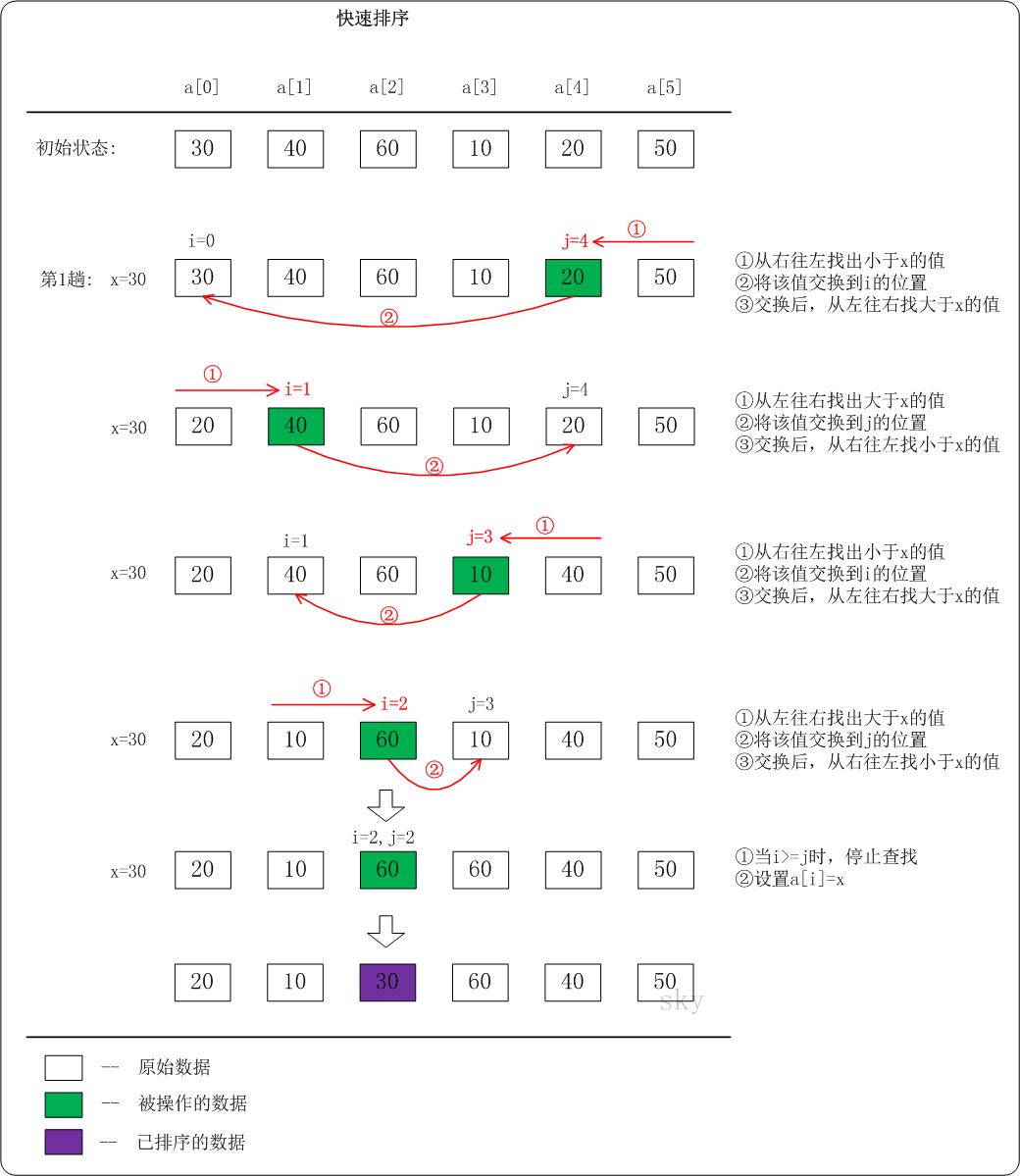
5. 快速排序

5.1 概述

快排的思路比较简单

  1. 拿到一段序列区间，从中取一个值当作pivot（比如说常见的取最左边元素）
  2. partition()方法负责将这段区间重新排列，小于pivot的在左边，大于的在右边
  3. 分别对左右两边递归进行快排，直至边界（left>=right）
  4. 快排最坏的情况下时间复杂度是${O(n^2)}$，比如当序列本身已经是有序的
  5. 虽然快排在最坏情况下会比归并排序慢，但是快排依然比归并排序用的更为广泛，其原因是：归并排序不是原地排序，所以，这里就有一个问题，我们的partition()方法可以有多种实现方式，但是如果选择非原地排序的实现方式，那快排就失去了相对于归并排序的优势

快排的复杂度分析：

  1. 在理想情况下，每次partition都有将序列分成平衡的两部分，此时的递归树是平衡的，时间复杂度也就是${O(nlogn)}$
  2. 在极端情况下，每次partition都将序列分成极不平衡的两部分，此时的递归树就变成了链表，时间复杂度也就变成了${O(n^2)}$
  3. 空间复杂度：如果partition选用原地排序的实现的话，空间复杂度主要就是递归栈的调用${O(logn)}$

5.1 最常见版本

public static void sort(int[] array) {
    System.out.println("普通版本快排");
    sort(array, 0, array.length - 1);
}
public static void sort(int[] array, int left, int right) {
    if (left < right) {
        int mid = partition(array,left,right);
        sort(array, left, mid - 1);
        sort(array, mid + 1, right);
    }
}
public static int partition(int[] nums, int left, int right) {
    int p1 = left;
    int p2 = right;
    int pivot = nums[left];
    // 先从右边走
    while (p1 < p2) {
        while (nums[p2] >= pivot && p1 < p2)
            p2--;
        while (nums[p1] <= pivot && p1 < p2)
            p1++;
        swap(nums, p1, p2);
    }
    swap(nums, left, p1);
    return p1;
}

5.2 单边法快排

partition()方法的另一种实现

// 单边法
public static int partition2(int[] nums,int left,int right){
    int pivot = nums[left];
    int p1 = left;
    int mid = left;
    for (int i = left; i <=right ; i++) {
        if(nums[i]<=pivot){
            swap(nums,i,p1++);
        }
    }
    for (int i = right; i >=left ; i--) {
        if (nums[i] < pivot) {
            mid = i;
            break;
        }
    }
    swap(nums,left,mid);
    return mid;
}

5.3 非递归方式

public static void sort3(int[] array) {
    System.out.println("非递归版本快排");
    sort3(array, 0, array.length - 1);
}
public static void sort3(int[] array, int left, int right) {
    if(left>=right)return;
    Stack<int[]> stack = new Stack<>();
    stack.push(new int[]{left,right});
    while (!stack.isEmpty()) {
        int[] cur =stack.pop();
        int l = cur[0];
        int r = cur[1];
        //这里是随便一个partition方法
        int mid = partition(array,l,r);
        if(l<mid-1)stack.push(new int[]{l,mid-1});
        if(mid<r-1)stack.push(new int[]{mid+1,r});
    }
}

6. 桶排序

6.1 复杂度分析

如果要排序的数据有 n 个，我们把它们均匀地划分到 m 个桶内，每个桶里就有 k=n/m 个元素。每个桶内部使用快速排序，时间复杂度为 O(k logk)。m 个桶排序的时间复杂度就是 O(m k logk)，因为 k=n/m，所以整个桶排序的时间复杂度就是 O(nlog(n/m))。当桶的个数 m 接近数据个数 n 时，log(n/m) 就是一个非常小的常量，这个时候桶排序的时间复杂度接近 O(n)。

在最坏的情况下，几乎所有元素都放在一个桶中，那时间复杂度就取决于桶内排序所采用的算法了

至于空间复杂度，首先有${k}$个桶需要占用${k}$个位置，额外需要${n}$个位置存放元素，所以就是${O(n+k)}$

6.2 适用场景

  • 数据要狠轻易划分成m个有顺序的桶
  • 数据的分布要均匀一点，否则时间复杂度就不是线性的了
  • 比较适合用在外部排序

6.2 代码

/**
 * @Classname BucketSort
 * @Description TODO
 * @Date 2019/12/6 18:37
 * @Created by Jesse
 */
public class BucketSort {
    public static void sort(double[] nums) {
        System.out.println("桶排序");
        //1. 得到最大值最小值，并计算出差值
        double max = nums[0];
        double min = nums[1];
        for (double item :
                nums) {
            max = Math.max(max, item);
            min = Math.min(min, item);
        }
        double d= max-min;

        //2. 初始化桶
        int bucketNum = nums.length;
        ArrayList<LinkedList<Double>> bucketList = new ArrayList<>(bucketNum);
        for (int i = 0; i < bucketNum; i++) {
            bucketList.add(new LinkedList<>());
        }

        //3. 遍历原始数组，将每个元素放入桶中
        for (int i = 0; i < nums.length; i++) {
            // !!!!!为什么要除以 桶的数量-1 ？ 因为下标是从0开开始的
            int num = (int) ((nums[i]-min) * (bucketNum-1)/d);
            bucketList.get(num).add(nums[i]);
        }

        //4. 对每个桶内进行排序
        // 在元素分布相对均匀的情况下，所有桶的运算量之和是n
        for (int i = 0; i < bucketList.size(); i++) {
            Collections.sort(bucketList.get(i));
        }

        //5. 输出全部元素
        double[] sortedArray = new double[nums.length];
        int index = 0;
        for (LinkedList<Double> list :
                bucketList) {
            for (double item :
                    list) {
                sortedArray[index++] = item;
            }
        }
        for (int i = 0; i < nums.length; i++) {
            nums[i] = sortedArray[i];
        }
    }
}

7. 计数排序

/**
 * @Classname CountSort
 * @Description TODO
 * @Date 2019/12/6 18:14
 * @Created by SunCheng
 */
public class CountSort {
    public static void sort(int[] nums) {
        System.out.println("计数排序");

        //1. 得到数列的最大值和最小值，计算差值d
        int max = nums[0];
        int min = nums[0];
        for (int item :
                nums) {
            max = max > item ? max : item;
            min = min < item ? min : item;
        }
        int d = max-min;
        //2. 创建统级数组，并统计对应元素的个数
        int[] countArray = new int[d + 1];
        for (int item :
                nums) {
            countArray[item-min]++;
        }

        //3. 统计数组变形，后面的元素等于前面的元素之和
        for (int i = 1; i < countArray.length; i++) {
            countArray[i]+=countArray[i-1];
        }
        //4. 倒序遍历数组，从统计数组找到正确位置，输出结果到数组
        // !!!!!!!倒序遍历是为了保证有序性，正序的话就无法保证了
        int[] sortedArray = new int[nums.length];
        for (int i = nums.length-1; i >=0 ; i--) {
            sortedArray[countArray[nums[i]-min]-1] = nums[i];
            countArray[nums[i]-min]--;
        }

        for (int i = 0; i < nums.length; i++) {
            nums[i] = sortedArray[i];
        }
    }
}

8. 基数排序

8.1 概述

基数排序的思想是，针对每一位，我们可以用计数排序等线性且稳定的排序进行排序，当对K位都处理完之后，整个数组也就处理完了

8.2 复杂度分析

时间复杂度：显然对K位分别进行计数排序，所以时间复杂度就是${O(n\times k)}$
空间复杂度：对于K位的数字，我们需要一个长度为K的数组countArray，又因为计数排序不属于原地排序，所以还需要一个长度为n的临时数组，故空间复杂度是${O(n+k)}$

8.3 代码

/**
 * @Classname RadixSort
 * @Description 基数排序
 * @Date 2019/12/16 9:25
 * @Created by SunCheng
 */
public class RadixSort {
    public static void sort(int[] nums) {
        System.out.println("基数排序");
        // 假设输入的数字长度都相同
        // 如果不等长，可以加一步补0对齐的操作
        int length = String.valueOf(nums[0]).length();
        for (int i = length-1; i >=0; i--) {
            // 根据第i位进行排序
            countSort(nums, i);
        }
    }

    // 下面基本就是计数排序的思想，只是比较的不再是数组中的元素，而是数组中元素的某一位
    private static void countSort(int[] nums, int index) {
        int min = 9,max = 0;
        for (int num :
                nums) {
            int val = getNumByIndex(num, index);
            min = Math.min(val,min);
            max = Math.max(max,val);
        }

        int[] countArray = new int[max - min + 1];
        for (int num:
                nums) {
            int val = getNumByIndex(num, index);
            countArray[val-min]++;
        }

        for (int i = 1; i < countArray.length; i++) {
            countArray[i] += countArray[i - 1];
        }

        int[] temp = new int[nums.length];
        for (int i = nums.length-1; i >=0 ; i--) {
            int val = getNumByIndex(nums[i], index)-min;
            int position = countArray[val];
            temp[position-1] = nums[i];
            countArray[val]--;
        }

        System.arraycopy(temp,0,nums,0,nums.length);
    }

    // 获取数字的第index位
    private static int getNumByIndex(int num, int index) {
        int len = String.valueOf(num).length();
        num = num/(int)Math.pow(10, len-index-1);
        return num%10;
    }
}

9. 堆排序

9.1 概述

我们都知道堆的特性是可迅速获取堆中的最大值或者最小值，而堆排序的思路就是构建一个大顶堆，之后

  1. 取对顶元素，与数组末尾元素交换
  2. 对顶元素做下沉操作（注意边界已经减一了）
  3. 重复${n-1}$次之后，数组将变成有序

9.2 复杂度分析

时间复杂度：首先是堆的构建，时间复杂度是${O(nlogn)}$，之后的（n-1）次下沉操作也是${O(nlogn)}$，所以总的时间复杂度是${O(nlogn)}$；
空间复杂度：堆排序属于原地排序，所以空间复杂度是${O(1)}$

9.3 代码实现

/**
 * @Classname HeapSort
 * @Description TODO
 * @Date 2019/12/6 19:07
 * @Created by Jesse
 */
public class HeapSort {
    public static void sort(int[] array) {
        System.out.println("堆排序");
        heapify(array, (array.length - 2) / 2, array.length);
        for (int i = array.length - 1; i > 0; i--) {
            swap(array, i, 0);
            siftDown(array, 0, i);
        }
    }

    public static void siftDown(int[] array, int i, int len) {
        while (leftChild(i) < len) {
            int child = leftChild(i);
            if (child + 1 < len && array[child + 1] > array[child])
                child++;

            if (array[i] >= array[child])
                break;

            swap(array, i, child);
            i = child;
        }
    }

    public static int leftChild(int k) {
        return 2 * k + 1;
    }

    public static void heapify(int[] array, int begin, int len) {
        for (int i = begin; i >= 0; i--)
            siftDown(array, i, len);
    }
}

10. 希尔排序

10.1 概述

希尔排序的思路也很简单，我们依次选取不同的步长，然后做插入排序，对于不同步长组成的序列，我们就称之为增量序列，而希尔排序的复杂度是和增量序列有关的，而增量序列需要满足的条件是最终步长要是1

下面介绍两个常用的增量序列
1. 希尔序列
$$h_t = \lfloor N/2 \rfloor, \qquad h_k = \lfloor h_{k+1}/2 \rfloor$$
其中N为数组长度
2. Hibbard增量序列
$$1, 3, ..., 2^k-1$$

10.2 复杂度分析

使用不同的增量序列， 希尔排序会表现出不同的时间复杂度，所以希尔排序的复杂度是一个没有终结的问题

  • 使用希尔序列时，最坏情况的时间复杂度是${\theta(N^2)}$
  • 使用Hibbard增量序列时，最坏情况的时间复杂度是${\theta(N^{3/2})}$
  • Sedgewick提出了几种序列，最坏情况的是复杂度是${\theta(N^{4/3})}$

10.3 代码

/**
 * @Classname ShellSort
 * @Description TODO
 * @Date 2019/12/16 14:00
 * @Created by SunCheng
 */
public class ShellSort {
    public static void sort(int[] nums) {
        for (int gap = nums.length/2; gap >0 ; gap/=2) {
            for (int i = gap; i <nums.length ; i++) {
                int key = nums[i];
                int k = i-gap;
                while (k >= gap && nums[k] > key) {
                    nums[k + gap] = nums[k];
                    k-=gap;
                }
                nums[k] = key;
            }
        }
    }

    // 这里是为了说明一下增量序列并不是固定的
    public static void sort2(int[] nums) {
        int[] seq = {5, 3, 1};
        for (int i = 0; i < seq.length; i++) {
            int gap = seq[i];
            for (int j = gap; j <nums.length ; j++) {
                int key = nums[j];
                int k = j-gap;
                while (k >= gap && nums[k] > key) {
                    nums[k+gap] = nums[k];
                    k-=gap;
                }
                nums[k] = key;
            }
        }
    }
}
点赞
收藏
评论区
推荐文章
22 22
•
4年前
【排序算法动画解】排序介绍及冒泡排序
本文为系列专题的第12篇文章。1.2.3.4.5.6.7.8.9.10.11.本文先简单介绍一下什么是排序，然后再结合动画介绍暴力排序和冒泡排序。1.什么是排序？排序在日常生活中无处不在。比如考试成绩的排名、体育课的从低到高的队形、网购时按价格升序排列或降序排列等等。|姓名|学号|班级|成绩|||||
2409
0
0
helloworld_78018081 helloworld_78018081
•
3年前
最新美团点评Java团队面试题，感悟分享
1.笔试常见的问题？面试常见的问题上面给的面试题链接基本都有。我只提几点：1.写SQL：写SQL很常考察groupby、内连接和外连接。2.手写代码：手写代码一般考单例、排序、线程、消费者生产者。我建议排序算法除了冒泡排序，最好还能手写一种其他的排序代码。试想：如果一般面试者都写的冒泡排序，而你写的是快速排序/堆排序，肯定能给面试官留下不错的印象。
2948
0
0
威尔we 威尔we
•
4年前
golang 之快速排序
1、快速排序稳定性快速排序是不稳定的算法，它不满足稳定算法的定义。算法稳定性假设在数列中存在aiaj，若在排序之前，ai在aj前面；并且排序之后，ai仍然在aj前面。则这个排序算法是稳定的！2、快速排序
2314
0
0
徐小夕 徐小夕
•
4年前
程序员必备的几种常见排序算法和搜索算法总结
前言最近为了巩固一下自己的算法基础,又把算法书里的基本算法刷了一遍,特地总结一下前端工程师需要了解的排序算法和搜索算法知识,虽然还有很多高深算法需要了解,但是基础还是要好好巩固一下的.本文将以图文的形式为大家介绍如下算法知识,希望在读完之后大家能有所收获:冒泡排序及其优化选择排序插入排序归并排序快速排序顺序搜索二分搜索
1604
0
0
Wesley13 Wesley13
•
3年前
Java面试总结（排序算法）
1.冒泡排序算法描述：两两比较，大的放后面2.选择排序算法描述：在m元数组中找到最小值的位置，然后将最小值的位置和第n(n0,1,2,....m1)位的值对调，排序k次则m元数组中前k(k<m)位的值已经排序好，m元数组中前k位的值不需要再进行排序，此时需要排序的元素只有mk个3.插入排序算
830
0
0
Wesley13 Wesley13
•
3年前
C++经典算法题
41.AlgorithmGossip:基数排序法说明在之前所介绍过的排序方法，都是属于「比较性」的排序法，也就是每次排序时，都是比较整个键值的大小以进行排序。这边所要介绍的「基数排序法」（radixsort）则是属于「分配式排序」（distributionsort），基数排序
909
0
0
Wesley13 Wesley13
•
3年前
BFPRT线性查找算法
介绍：BFPRT算法解决的问题十分经典，即从某n个元素的序列中选出第k大（第k小）的元素，通过巧妙的分析，BFPRT可以保证在最坏情况下仍为线性时间复杂度。该算法的思想与快速排序思想相似，当然，为使得算法在最坏情况下，依然能达到o(n)的时间复杂度，五位算法作者做了精妙的处理。时间复杂度O(N)算法步骤
845
0
0
Stella981 Stella981
•
3年前
JavaScript常用基础算法
基础算法一、排序1.冒泡排序//冒泡排序functionbubbleSort(arr){for(vari1,lenarr.length;i<len1;i){for(varj0;j<
868
0
0
Stella981 Stella981
•
3年前
Lua 排序算法
冒泡排序（BubbleSort，台湾译为：泡沫排序或气泡排序）是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。算法步骤1.有一个长度为n
755
0
0
京东云开发者 京东云开发者
•
1年前
时间复杂度为 O (n^2) 的排序算法 | 京东物流技术团队
对于小规模数据，我们可以选用时间复杂度为O(n2)的排序算法。因为时间复杂度并不代表实际代码的执行时间，它省去了低阶、系数和常数，仅代表的增长趋势，所以在小规模数据情况下，O(n2)的排序算法可能会比O(nlogn)的排序算法执行效率高。不过随着数据规模增
405
0
0
京东云开发者 京东云开发者
•
8个月前
时间复杂度为 O(n^2) 的排序算法
作者：京东保险王奕龙对于小规模数据，我们可以选用时间复杂度为O(n2)的排序算法。因为时间复杂度并不代表实际代码的执行时间，它省去了低阶、系数和常数，仅代表的增长趋势，所以在小规模数据情况下，O(n2)的排序算法可能会比O(nlogn)的排序算法执行效率高
262
0
0
马邈
马邈
Lv1
春眠不觉晓，处处闻啼鸟。夜来风雨声，花落知多少！
文章
7
粉丝
0
获赞
0
热门文章
JVS低代码权限管控方式
带你探索JUnit 5.4
node入门基础
ClickHouse（1）- 分布式架构
如何成为更好的AI专业人员？请查收这7条实战经验