前言
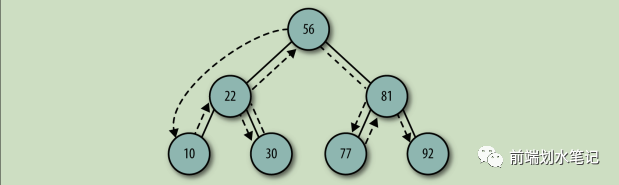
堆(二叉堆),一种动态的树型结构,一种除了底层外,完全被填满的二叉树结构。因此,堆一般是基于数组去实现的,它不会出现数组中很多空缺的现象,而造成空间浪费。如下是一个完全二叉树: 
它可以用数组表示为[10,7,2,5,1],若以k表示当前数组的索引,那么:
- 其父节点:
floor((k-1)/2) - 其左孩子:
2k+1 - 其又孩子:
2k+2
结合上图,堆的性质如下:
- 堆必须是完全二叉树;
- 任一节点要么比其子树节点大,要么小;
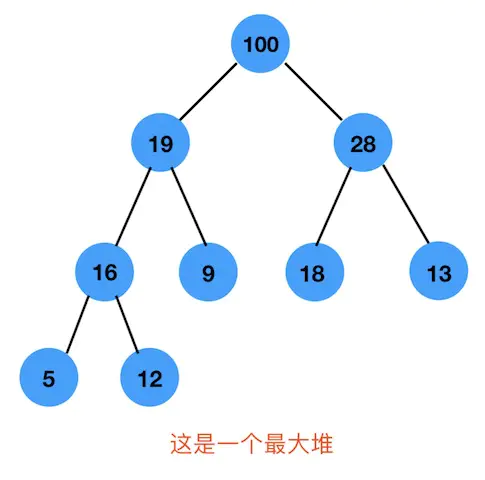
- 根据上面性质,堆被分为最大堆(大顶堆)和最小堆(小顶堆)。
堆的主要用途:
- 构建优先队列;
- 支持堆排序;
- 快速找出集合中的最大值或最小值。
堆结构的基本操作(以最大堆为例,本文均使用vector容器存储数组,假设vector容器的基本操作时间复杂度为Θ(1)):
-
MaxHeap:维护最大堆的性质,时间复杂度O(nlgn); -
BuildHeap:从无序的输入数据构造一个最大堆,时间复杂度为O(n);
堆结构的基本操作
1.MaxHeap:
输入一个数组A和一个下标i,使不满足最大堆性质的A[i]逐级下降,直到满足。
void MaxHeap(vector<int> &A, int i){
int max; //存储父节点和其子树节点中的最大值下标
int lef_child = 2i; //左孩子
int rig_child = 2i + 1; //右孩子
//左孩子大于父节点
if(lef_child <= A.size() && A[lef_child] > A[i])
max = lef_child;
else max = i;
//右孩子更大
if(rig_child <= A.size() && A[rig_child] > A[max])
max = rig_child;
//将最大值上移至父节点
if(max != i){
//交换
int temp = A[i]; A[i] = A[max]; A[max] = temp;
//更新了数组,需继续查看当前元素是否满足最大堆性质
MaxHeap(A, max);
}
}因为每一个节点的子树节点数(包括孩子的孩子)至多为2n/3(n是整个树的节点数,最坏情况即节点为根节点,且底层大于等于半满),所以该算法的时间复杂度为T(n) <= T(2n/3) + Θ(1)通过主方法求解得T(n)=O(lgn),最后因为含n个元素的堆高为O(lgn),所以其时间复杂度又可以表示为O(h)。
2.BuildHeap:
可以通过自底向上的方法,从最后一个叶节点开始倒序遍历,并调用MaxHeap判断当前节点子树是否满足最大堆性质。
void BuildHeap(vector<int> &A){
int i = A.size()/2; //最后一个非叶节点的位置
for(i; i >= 0; i--) //自底向上维护
MaxHeap(A, i);
}该算法的时间复杂度很容易通过,循环n次,每次调用MaxHeap耗费O(lgn),从而得出T(n)=O(nlgn),虽然正确,但是该算法上界还可以继续紧确。
一个含n个元素的堆高(最底层高为0)为floor(lgn),而该堆最多包含ceil(n/2^(h+1))个高度为h的节点。而一个高度为h的节点运行MaxHeap的时间复杂度为O(h),所以可以将BuildHeap的总代价表示为: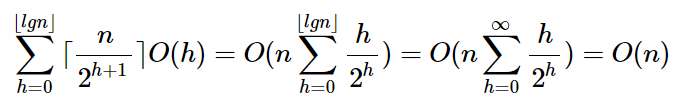
构建一个优先队列
1.什么是优先队列
优先队列是一种特殊的队列,它不按先进先出的原则,而是以优先度来弹出元素。它本质是一种用来维护由一组元素构成的集合S的数据结构,其中每个元素都有一个相关的值,称为关键字。和堆一样,优先队列也分为最大优先队列和最小优先队列。
2.优先队列的相关操作
HeapTop: 返回并删除掉当前堆顶,时间复杂度为O(lgn)。
int HeapTop(vector<int> &A){
if(A.size() < 1) exit(0); //没有元素
int max = A[0];
//堆顶等于最后一个值,并将最后一个值弹出
A[0] = A[A.size()-1];
A.push_pop();
//维护最大堆性质
MaxHeap(A, 0);
return max;
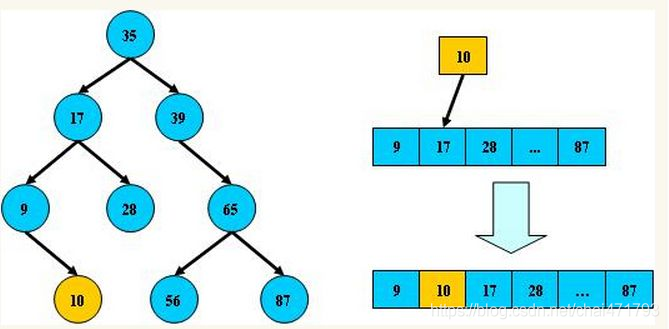
}HeapInsert:插入一个元素到当前堆中,时间复杂度为O(lgn)。
void HeapInsert(vector<int> &A, k){
A.push_back(A[0]);
A[0] = k;
//维护最大堆性质
MaxHeap(A, 0);
}STL中堆与优先队列的实现
1.堆
heap不属于STL中的容器组件,它是以算法的形式呈现,“默默扮演着幕后英雄”。heap默认是最大堆排序。使用方法如下:
vector<int> ivec{0, 1, 2};
//最大堆[2, 1, 0]
make_heap(ivec.begin(), ivec.end());
ivec.push_back(5);
//在堆的基础上进行数据插入[5, 2, 0, 1]
push_heap(ivec.begin(), ivec.end());
//pop_heap并没有删除元素,而是将堆顶元素与最后一个元素进行了替换
//[2, 1, 0, 5]
pop_heap(ivec.begin(), ivec.end());
//删除堆顶的元素[2, 1, 0]
ivec.pop_back();
//默认小堆排序[0, 1, 2]
sort_heap(ivec.begin(), ivec.end());2.优先队列
priority_queue是STL中优先队列的名称,默认也是最大堆排序。使用方法如下:
priority_queue<int> que;
que.push(x); //每次push之后会自动维护,保证堆顶是优先级别最高的
que.pop();
que.top();priority_queue还可以自定义存储的数据类型以及排序方式,具体应用可以【关注公众号DoCode,每日一道LeetCode,将零碎时间利用起来】回复关键字“堆”查看。