基于活动选择问题的贪心算法 - HelloWorld开发者社区

问题描述:

Coda从0时刻开始观看直播，到 t 时刻结束。一共有n场直播可被选择，已知所有直播场次的起止时间和主播名称，其中第i场直播从ai时刻开始，bi时刻结束，主播名称为ci，每场直播的起始时间和结束时间都是整点（不保证所有直播全程都在Coda观看的时间段内)。Coda同时只能观看一场直播,并且必须看完正在观看的直播，才能选择下一场尚未开始的直播。

请求出Coda在这段时间内最多能观看几场直播，并按照观看顺序输出观看的每个主播的名称。

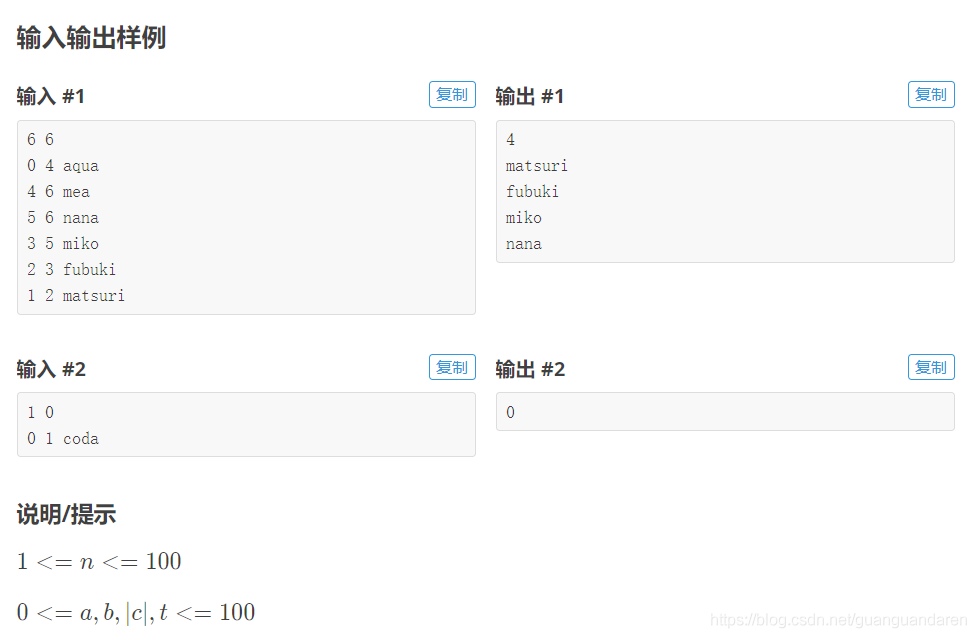
输入格式

第一行包含两个整数ｎ和t，分别表示已知的直播场数和结束观看的时刻。

接下来n行，每行包含两个整数a和b，以及一个由小写字母组成的字符串c，分别表示每场直播的起始时间，结束时间，主播名称。

输出格式

第一行包含一个整数，输出最多能观看多少场直播。

接下来n行，每行输出一个字符串，按照观看顺序输出所看主播的名称。

)

这是一个经典的活动选择问题：

给出n个活动的开始时间和结束时间，同一时间只能参与一个活动，要找出可以参与的最多活动的个数。

题目老贪心了。我们知道，贪心算法会在每一步中直接选择当前看来最好的选择。在求解过程中，选择一个活动方法最优解，然后对剩余的子问题（包含与已选择的活动兼容的活动）进行求解。

贪心算法通常都是这种自顶向下的设计：做出一个选择，然后求解剩下的那个子问题，而不是自底向上求解出很多子问题，然后再做出选择。

算法描述

（如果分析或证明看不懂可直接点击前往算法图示部分）

基于活动选择的贪心策略，能得出以下定理：

对于任意非空子问题Sij，设am是Sij中具有最早结束时间的活动，那么

（1）活动am在Sij中的某最大兼容活动子集中被使用。

（2）子问题Sim为空，所以选择am将使子问题Smj为唯一可能非空的子问题。

假定有一个n个活动的集合S={a1,a2,a3...,an}，
这些活动使用同一个资源（例如同一个阶梯教室），而这个资源在某个时刻只能供一个活动使用。每个活动ai都有一个开始时间si和一个结束时间fi，设当前时间为now,占用资源结束时间为t
其中now<=si<fi<=t。如果被选中，任务ai发生在半开时间区[si,fi)期间。如果两个活动ai和aj满足[si,fi)和[sj,fj)不重叠，则称它们是兼容的。
若si>=fj，或sj>=fi，则ai和j是兼容的。在活动选择问题中，我们希望选出一个最大兼容活动集。

在最开始时选出结束时间最早的那个活动，就能够为其他活动尽可能地腾出更多时间。而后，每一步都在剩下的活动中选取，也遵循类似的原则。

因此，我们要选择活动中结束时间最早并且开始时间大于或等于先前所选活动的结束时间的下一个活动。

即：Step①：根据活动结束时间对活动递增排序；

　　Step②：对排序后的活动，如果开始时间大于或等于上一个选中活动的结束时间（初始活动时间为０），则选中该活动。

算法分析

对于给定的一组活动为S = {1,2,3，.. n}，并且已按活动结束时间对所有活动进行排序。贪心策略总是选择【活动1】。为什么【活动1】始终是最佳解决方案之一？下面给出简单的证明：

假设存在除了【活动1】以外的另一个最佳解决方案S，并且S选择的第一个活动是【活动k】，而不是【活动1】。现在我们来说明，把【活动k】替换成【活动1】，得到的新方案S‘，{B-{k}}U{1}，必定仍然是一个最佳解决方案，说明如下：因为S 中的活动是独立的，而在排序队列中，【活动1】在所有活动中具有最小的结束时间，因为k不等于1，【活动k】的完成时间必定是大于等与【活动1】的完成时间，因此把【活动k】换成【活动1】后的新方案S‘必定也是最佳解决方案。

算法图示

看不懂没关系(我也).请参考我随手画的图，也许不严谨，但将尽可能直观。

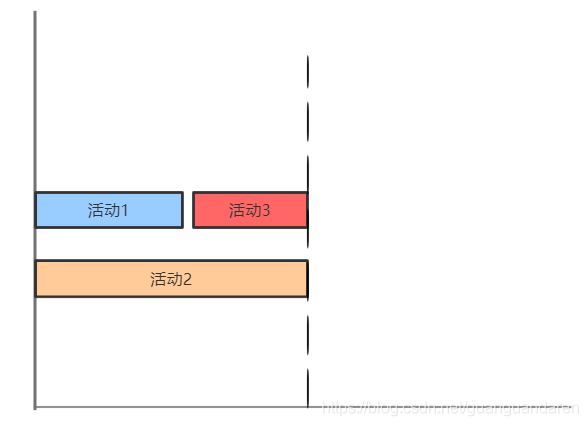
Case1：活动２与活动３的结束时间相同

基于活动选择问题的贪心算法 )

（不要小看图中的虚线，虚线表示的是每个活动的结束时间，虽然挺丑的,但每次做选择的时候都得通过这一条条虚线划分区域）

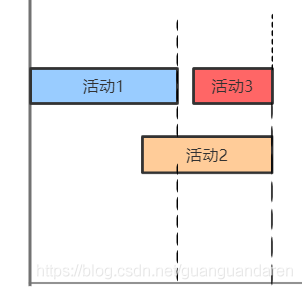
由于题目要求活动按时间顺序输出，因此活动2的起始时间在活动1的起始时间和结束时间之间的情况都是一样的，即与下图的情况等价

基于活动选择问题的贪心算法 )

显然，先选择活动１为后面腾出多余的时间。此时活动１与活动３属于活动２的活动时间范围内的子集（即能够选择活动２，必能选择活动１＋活动３）。

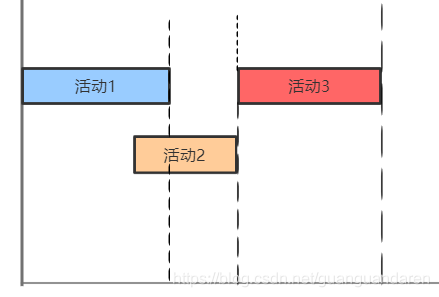
Case2：活动3结束时间晚于活动2结束时间

基于活动选择问题的贪心算法 )

或许在这种情况下你无法确定该选出哪个活动，至少可以说：活动2看起来也不差?那么我们引入一个新的活动4

基于活动选择问题的贪心算法 )

这里其实我们很容易地可以做出以下决定：

①只要活动2的结束时间晚于活动1，选择活动1后总是能够选择活动3或活动4。因此选择活动1是第一步的最优解。

②选出活动1以后可以将活动2给去掉。即

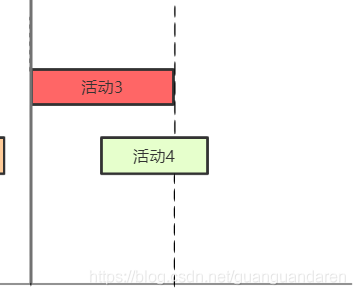基于活动选择问题的贪心算法 )

我们可以发现，选出活动1后，在剩下能够选择的活动中又回到了上一次做决定时面对的情况。

这时只要继续选出结束时间更早的活动，就是题目的最优解。(如果结束时间相同，按照先来先进行即可)

以下图为例

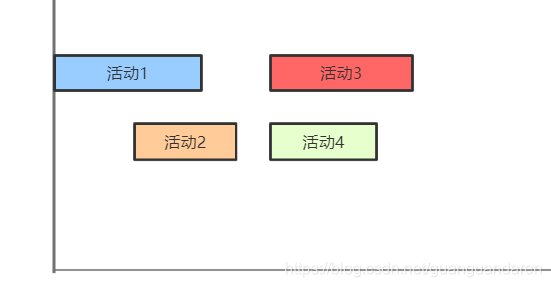基于活动选择问题的贪心算法 )

首先,将每个活动按结束时间递增排序。我们将选出1,然后去掉2,选中4,然后去掉3......

附此题代码:

#include <bits/stdc++.h>
using namespace std;
typedef pair<int, string> p;
typedef pair<int, p> Acti; //活动结构体
int main()
{
    int n, t, a, b, end = 0; //end是当前活动时间,初始值为0,起始时间大于或等于当前时间的活动均为可选活动
    cin >> n >> t;
    Acti activities[n];
    string ans[n];
    for (int i = 0; i < n; i++)
        cin >> activities[i].second.first >> activities[i].first >> activities[i].second.second;
    sort(activities, activities + n);//step1:对活动的结束时间排序(因为需要按起始时间顺序输出,就直接把整个结构体排了吧)
    int count = 0;
    for (int i = 0; i < n; i++)                
        if (activities[i].second.first >= end) //step2:对排序后的活动，如果开始时间大于或等于上一个选中活动的结束时间,则选出该活动.
        {
            if (activities[i].first > t) //当活动中的结束时间大于活动结束的时刻就停止
                break;
            ans[count++] = activities[i].second.second;
            end = activities[i].first; //当前活动时间更新
        }
    cout << count << endl;
    for (int i = 0; i < count; i++)
        cout << ans[i] << endl;
}

本文转自 https://blog.csdn.net/guanguandaren/article/details/107911535，如有侵权，请联系删除。