读完本文，你不仅学会了算法套路，还可以顺便去 LeetCode 上拿下如下题目：

380.常数时间插入、删除和获取随机元素

710.黑名单中的随机数

-----------

本文讲两道比较有技巧性的数据结构设计题，都是和随机读取元素相关的，我们前文 水塘抽样算法 也写过类似的问题。

这写问题的一个技巧点在于，如何结合哈希表和数组，使得数组的删除操作时间复杂度也变成 O(1)？

下面来一道道看。

实现随机集合

这是力扣第 380 题，看下题目：

就是说就是让我们实现如下一个类：

class RandomizedSet {
public:
    /** 如果 val 不存在集合中，则插入并返回 true，否则直接返回 false */
     bool insert(int val) {}
    
    /** 如果 val 在集合中，则删除并返回 true，否则直接返回 false */
    bool remove(int val) {}
    
    /** 从集合中等概率地随机获得一个元素 */
    int getRandom() {}
}

本题的难点在于两点：

1、插入，删除，获取随机元素这三个操作的时间复杂度必须都是 O(1)。

2、getRandom 方法返回的元素必须等概率返回随机元素，也就是说，如果集合里面有 n 个元素，每个元素被返回的概率必须是 1/n。

我们先来分析一下：对于插入，删除，查找这几个操作，哪种数据结构的时间复杂度是 O(1)？

HashSet 肯定算一个对吧。哈希集合的底层原理就是一个大数组，我们把元素通过哈希函数映射到一个索引上；如果用拉链法解决哈希冲突，那么这个索引可能连着一个链表或者红黑树。

那么请问对于这样一个标准的 HashSet，你能否在 O(1) 的时间内实现 getRandom 函数？

其实是不能的，因为根据刚才说到的底层实现，元素是被哈希函数「分散」到整个数组里面的，更别说还有拉链法等等解决哈希冲突的机制，基本做不到 O(1) 时间等概率随机获取元素。

除了 HashSet，还有一些类似的数据结构，比如哈希链表 LinkedHashSet，我们前文 手把手实现LRU算法 和 手把手实现LFU算法 讲过这类数据结构的实现原理，本质上就是哈希表配合双链表，元素存储在双链表中。

但是，LinkedHashSet 只是给 HashSet 增加了有序性，依然无法按要求实现我们的 getRandom 函数，因为底层用链表结构存储元素的话，是无法在 O(1) 的时间内访问某一个元素的。

根据上面的分析，对于 getRandom 方法，如果想「等概率」且「在 O(1) 的时间」取出元素，一定要满足：底层用数组实现，且数组必须是紧凑的。

这样我们就可以直接生成随机数作为索引，从数组中取出该随机索引对应的元素，作为随机元素。

但如果用数组存储元素的话，插入，删除的时间复杂度怎么可能是 O(1) 呢？

可以做到！对数组尾部进行插入和删除操作不会涉及数据搬移，时间复杂度是 O(1)。

所以，如果我们想在 O(1) 的时间删除数组中的某一个元素 val，可以先把这个元素交换到数组的尾部，然后再 pop 掉。

交换两个元素必须通过索引进行交换对吧，那么我们需要一个哈希表 valToIndex 来记录每个元素值对应的索引。

有了思路铺垫，我们直接看代码：

class RandomizedSet {
public:
    // 存储元素的值
    vector<int> nums;
    // 记录每个元素对应在 nums 中的索引
    unordered_map<int,int> valToIndex;
    
    bool insert(int val) {
        // 若 val 已存在，不用再插入
        if (valToIndex.count(val)) {
            return false;
        }
        // 若 val 不存在，插入到 nums 尾部，
        // 并记录 val 对应的索引值
        valToIndex[val] = nums.size();
        nums.push_back(val);
        return true;
    }
     
    bool remove(int val) {
        // 若 val 不存在，不用再删除
        if (!valToIndex.count(val)) {
            return false;
        }
        // 先拿到 val 的索引
        int index = valToIndex[val];
        // 将最后一个元素对应的索引修改为 index
        valToIndex[nums.back()] = index;
        // 交换 val 和最后一个元素
        swap(nums[index], nums.back());
        // 在数组中删除元素 val
        nums.pop_back();
        // 删除元素 val 对应的索引
        valToIndex.erase(val);
        return true;
    }
    
    int getRandom() {
        // 随机获取 nums 中的一个元素
        return nums[rand() % nums.size()];
    }
};

注意 remove(val) 函数，对 nums 进行插入、删除、交换时，都要记得修改哈希表 valToIndex，否则会出现错误。

至此，这道题就解决了，每个操作的复杂度都是 O(1)，且随机抽取的元素概率是相等的。

避开黑名单的随机数

有了上面一道题的铺垫，我们来看一道更难一些的题目，力扣第 710 题，我来描述一下题目：

给你输入一个正整数 N，代表左闭右开区间 [0,N)，再给你输入一个数组 blacklist，其中包含一些「黑名单数字」，且 blacklist 中的数字都是区间 [0,N) 中的数字。

现在要求你设计如下数据结构：

class Solution {
public:
    // 构造函数，输入参数
    Solution(int N, vector<int>& blacklist) {}
    
    // 在区间 [0,N) 中等概率随机选取一个元素并返回
    // 这个元素不能是 blacklist 中的元素
    int pick() {}
};

pick 函数会被多次调用，每次调用都要在区间 [0,N) 中「等概率随机」返回一个「不在 blacklist 中」的整数。

这应该不难理解吧，比如给你输入 N = 5, blacklist = [1,3]，那么多次调用 pick 函数，会等概率随机返回 0, 2, 4 中的某一个数字。

而且题目要求，在 pick 函数中应该尽可能少调用随机数生成函数 rand()。

这句话什么意思呢，比如说我们可能想出如下拍脑袋的解法：

int pick() {
    int res = rand() % N;
    while (res exists in blacklist) {
        // 重新随机一个结果
        res = rand() % N;
    }
    return res;
}

这个函数会多次调用 rand() 函数，执行效率竟然和随机数相关，不是一个漂亮的解法。

聪明的解法类似上一道题，我们可以将区间 [0,N) 看做一个数组，然后将 blacklist 中的元素移到数组的最末尾，同时用一个哈希表进行映射：

根据这个思路，我们可以写出第一版代码（还存在几处错误）：

class Solution {
public:
    int sz;
    unordered_map<int, int> mapping;
    
    Solution(int N, vector<int>& blacklist) {
        // 最终数组中的元素个数
        sz = N - blacklist.size();
        // 最后一个元素的索引
        int last = N - 1;
        // 将黑名单中的索引换到最后去
        for (int b : blacklist) {
            mapping[b] = last;
            last--;
        }
    }
};

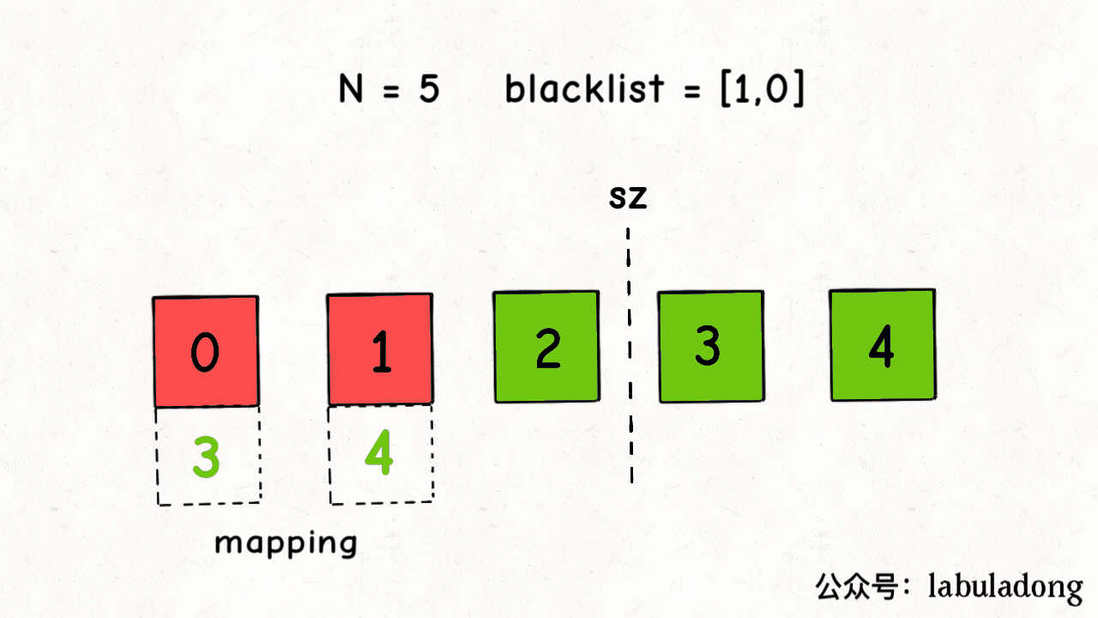
如上图，相当于把黑名单中的数字都交换到了区间 [sz, N) 中，同时把 [0, sz) 中的黑名单数字映射到了正常数字。

根据这个逻辑，我们可以写出 pick 函数：

int pick() {
    // 随机选取一个索引
    int index = rand() % sz;
    // 这个索引命中了黑名单，
    // 需要被映射到其他位置
    if (mapping.count(index)) {
        return mapping[index];
    }
    // 若没命中黑名单，则直接返回
    return index;
}

这个 pick 函数已经没有问题了，但是构造函数还有两个问题。

第一个问题，如下这段代码：

int last = N - 1;
// 将黑名单中的索引换到最后去
for (int b : blacklist) {
    mapping[b] = last;
    last--;
}

我们将黑名单中的 b 映射到 last，但是我们能确定 last 不在 blacklist 中吗？

比如下图这种情况，我们的预期应该是 1 映射到 3，但是错误地映射到 4：

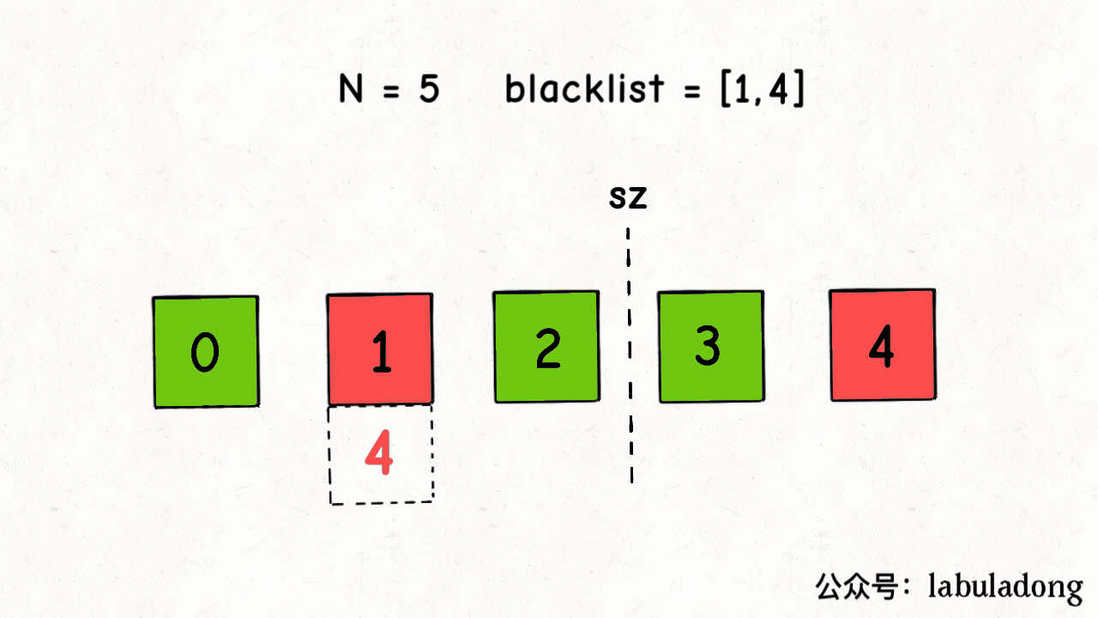
在对 mapping[b] 赋值时，要保证 last 一定不在 blacklist 中，可以如下操作：

// 构造函数
Solution(int N, vector<int>& blacklist) {
    sz = N - blacklist.size();
    // 先将所有黑名单数字加入 map
    for (int b : blacklist) { 
        // 这里赋值多少都可以
        // 目的仅仅是把键存进哈希表
        // 方便快速判断数字是否在黑名单内
        mapping[b] = 666;
    }

    int last = N - 1;
    for (int b : blacklist) {
        // 跳过所有黑名单中的数字
        while (mapping.count(last)) {
            last--;
        }
        // 将黑名单中的索引映射到合法数字
        mapping[b] = last;
        last--;
    }
}

第二个问题，如果 blacklist 中的黑名单数字本身就存在区间 [sz, N) 中，那么就没必要在 mapping 中建立映射，比如这种情况：

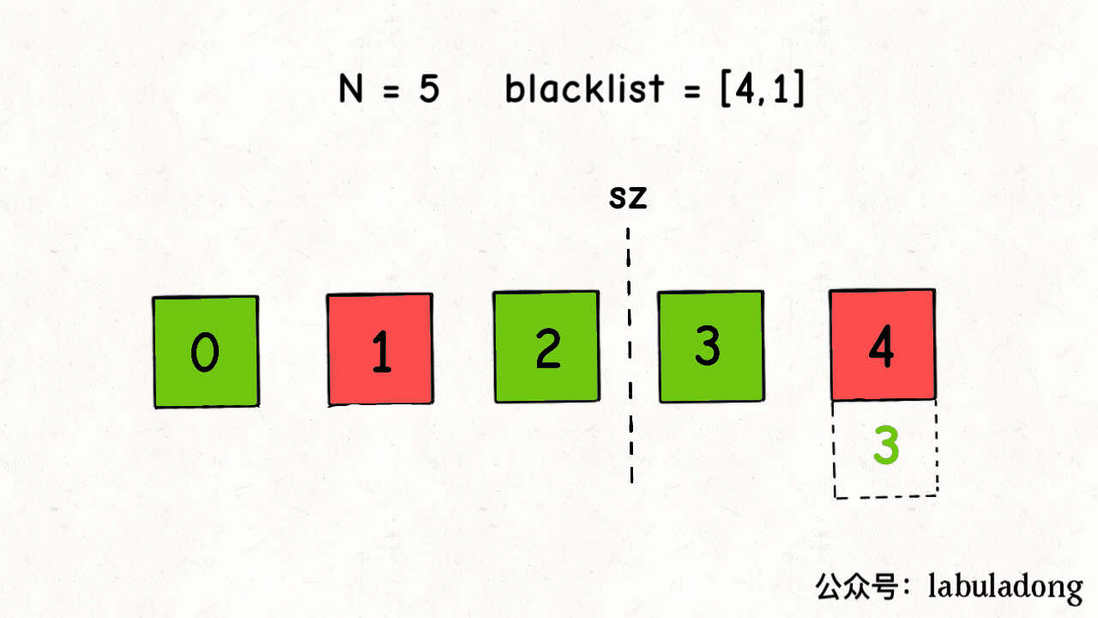
我们根本不用管 4，只希望把 1 映射到 3，但是按照 blacklist 的顺序，会把 4 映射到 3，显然是错误的。

我们可以稍微修改一下，写出正确的解法代码：

class Solution {
public:
    int sz;
    unordered_map<int, int> mapping;
    
    Solution(int N, vector<int>& blacklist) {
        sz = N - blacklist.size();
        for (int b : blacklist) {
            mapping[b] = 666;
        }

        int last = N - 1;
        for (int b : blacklist) {
            // 如果 b 已经在区间 [sz, N)
            // 可以直接忽略
            if (b >= sz) {
                continue;
            }
            while (mapping.count(last)) {
                last--;
            }
            mapping[b] = last;
            last--;
        }
    }

    // 见上文代码实现
    int pick() {}
};

至此，这道题也解决了，总结一下本文的核心思想：

1、如果想高效地，等概率地随机获取元素，就要使用数组作为底层容器。

2、如果要保持数组元素的紧凑性，可以把待删除元素换到最后，然后 pop 掉末尾的元素，这样时间复杂度就是 O(1) 了。当然，我们需要额外的哈希表记录值到索引的映射。

3、对于第二题，数组中含有「空洞」（黑名单数字），也可以利用哈希表巧妙处理映射关系，让数组在逻辑上是紧凑的，方便随机取元素。