红黑树代码分析C/C++（参考自零声学院）

1. 红黑树的定义：

定义：
- 每个结点是红的或者黑的；
- 根结点是黑的；
- 每个叶子结点是黑的；
- 如果一个结点是红的，则它的两个儿子都是黑的；
- 对每个结点，从该结点到其子孙结点的所有路径上的包含相同数目的黑结点；
2. 左旋and右旋

代码：

void rbtree_left_rotation(rbtree* T, rbtree_node* x) {
  if (x == T->nil) return;
  rbtree_node* y = x->right;

  if (y == T->nil) return;

  // 3.1 
  x->right = y->left;
  if (y->left != T->nil) {
      y->left->parent = x;
  }

  // 3.2 
  y->parent = x->parent;
  if (x->parent == T->nil) {
      T->root = y;
  } else if (x == x->parent->left) {
      x->parent->left = y;
  } else if (x == x->parent->right) {
      x->parent->right = y;
  }

  // 3.3 
  y->left = x;
  x->parent = y;
}

void rbtree_right_rotation(rbtree* T, rbtree_node* y) { if (y == T->nil) return; rbtree_node* x = y->left;

if (x == T->nil) return;

// 3.1 
y->left = x->right;
if (x->right != T->nil) {
    x->right->parent = y;
}

// 3.2 
x->parent = y->parent;
if (y->parent == T->nil) {
    T->root = x;
} else if (y == y->parent->left) {
    y->parent->left = x;
} else if (y == y->parent->right) {
    y->parent->right = x;
}

// 3.3
x->right = y;
y->parent = x;

}


**3. 红黑树插入情况分析：**

- 插入节点的位置默认为：**叶子节点处**

- 插入节点的颜色默认为：**红色**

- **情况1：**

  - 插入节点的**父节点**为**黑色**，不用做任何处理
- **情况2：**
  - **插入节点的父节点为红色：**

    - **父节点是祖父节点的左子树：**

      - **叔父节点是红色：**

        - 把父节点和叔父节点变为黑色，并且把祖父节点变为红色，这时在递归判断祖父节点

        ![image (1)](https://img-hello-world.oss-cn-beijing.aliyuncs.com/imgs/d5edb08a25b5c68323f82243cbb99080.png)

      - **叔父节点为黑色：**

        - **当前插入节点为右孩子：**

          - 左旋+右旋

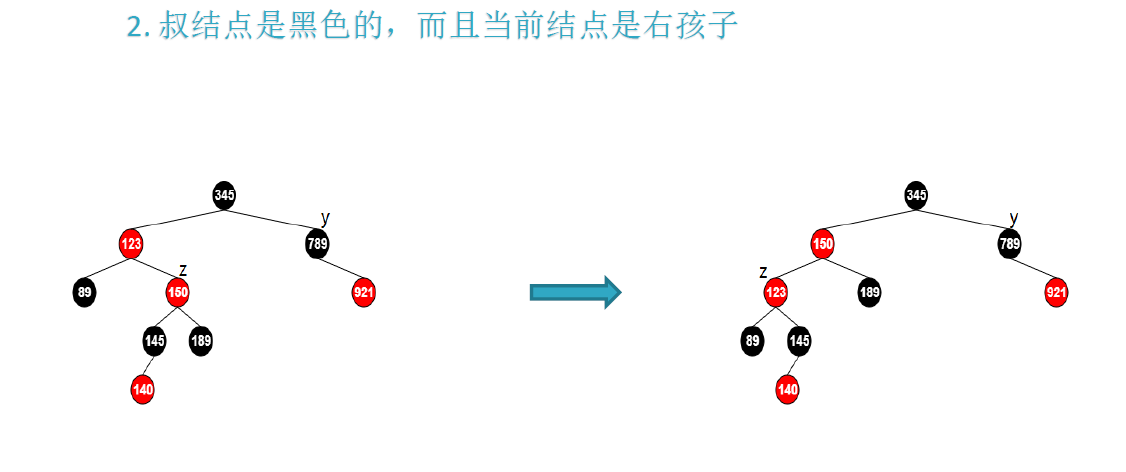
          ![image (2)](https://img-hello-world.oss-cn-beijing.aliyuncs.com/imgs/955d98611b3dc930c48da97654949d35.png)

          ![image (3)](https://img-hello-world.oss-cn-beijing.aliyuncs.com/imgs/26df59625bd2f3a6971155489b7fbf80.png)

        - **当前插入节点为左孩子：**

          - 右旋

          ![image (3)](https://img-hello-world.oss-cn-beijing.aliyuncs.com/imgs/1e5842b2ef140ec4845c9b548d2263b4.png)

    - **父节点是祖父节点的右子树：**

      - **叔父节点是红色：**

        - 把父节点和叔父节点变为黑色，并且把祖父节点变为红色，这时在递归判断祖父节点

      - **叔父节点为黑色：**

        - **当前插入节点为左孩子：**

          - 右旋+左旋

        - **当前插入节点为右孩子：**

          - 左旋

- **代码：**
``` // 4. 红黑树的插入
void rbtree_insert_fixup(rbtree* T, rbtree_node* node) {
    // 只有父节点也是红色节点的时，才需要调整
    while (node->parent->color == RED) {
        // 4.1 父节点是爷爷节点的左子树
        if (node->parent == node->parent->parent->left) {
            rbtree_node* uncle_node = node->parent->parent->right;

            // 4.1.1 叔父节点是红色节点
            if (uncle_node->color == RED) {
                node->parent->parent->color = RED;
                node->parent->color = BLACK;
                uncle_node->color = BLACK;

                node = node->parent->parent;

            // 4.1.2 叔父节点是黑色节点
            } else if (uncle_node->color == BLACK) {
                if (node == node->parent->right) {
                    node = node->parent;
                    rbtree_left_rotation(T, node);
                }

                node->parent->color = BLACK;
                node->parent->parent->color = RED;
                rbtree_right_rotation(T, node->parent->parent);
            }

        // 4.2 父节点是爷爷节点的右子树
        } else if (node->parent == node->parent->parent->right) {
            rbtree_node* uncle_node = node->parent->parent->left;

            // 4.2.1 叔父节点是红色节点
            if (uncle_node->color == RED) {
                node->parent->parent->color = RED;
                node->parent->color = BLACK;
                uncle_node->color = BLACK;

                node = node->parent->parent;

            // 4.2.2 叔父节点是黑色节点
            } else if (uncle_node->color == BLACK) {
                if (node == node->parent->left) {
                    node = node->parent;
                    rbtree_right_rotation(T, node);
                }

                node->parent->color = BLACK;
                node->parent->parent->color = RED;
                rbtree_left_rotation(T, node->parent->parent);
            }
        }
    }

    T->root->color = BLACK;
}

void rbtree_insert(rbtree* T, rbtree_node* node) {
    // 4.1 找到插入位置的父节点
    rbtree_node* x = T->root;
    rbtree_node* y = T->nil;

    while (x != T->nil) {
        y = x;

        if (node->key == x->key) {
            return;    // 一样，不做处理
        } else if (node->key < x->key) {
            x = x->left;
        } else if (node->key > x->key) {
            x = x->right;
        }
    }

    // 4.2 插入
    node->parent = y;
    if (y == T->nil) {
        T->root = node;
    } else if (y->key > node->key) {
        y->left = node;
    } else if (y->key < node->key) {
        y->right = node;
    }

    node->left = T->nil;
    node->right = T->nil;
    node->color = RED;    // 默认插入红色

    // 4.3 调整
    rbtree_insert_fixup(T, node);
}

4. 红黑树删除情况分析：

删除：
- 情况1：待删除节点的左右子树，都为空
  - 直接删除该节点
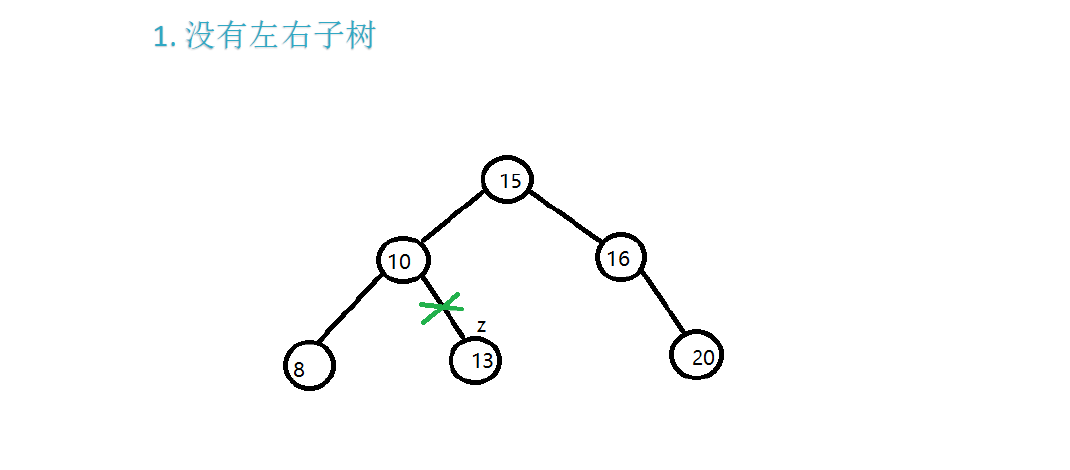
- 情况2：待删除节点的左右子树，1个为空、1个不为空
  - 直接删除该节点，并让该节点的父节点，指向其左子树or右子树
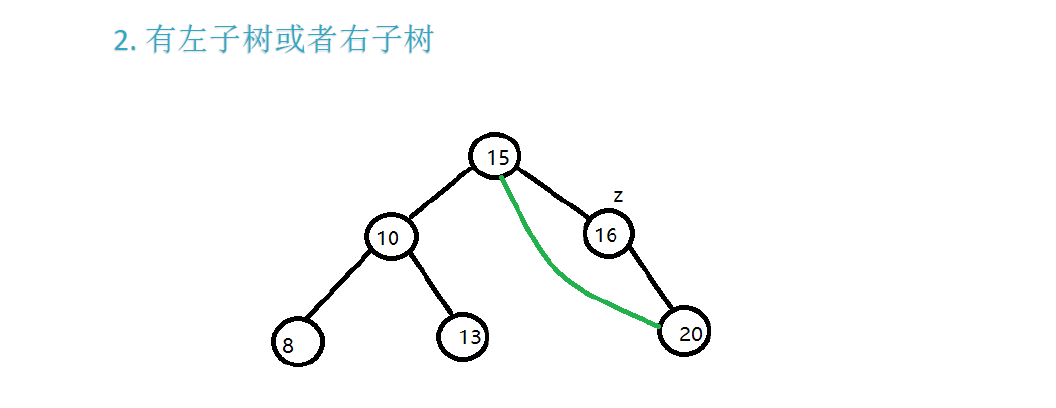
- 情况3：待删除节点的左右子树，都不为空
  - 找到该待删除的节点的可代替节点，左子树的最大值or右子树的最小值
  - 删除该可代替节点
  - 并用可代替节点，覆盖真正待删除的节点
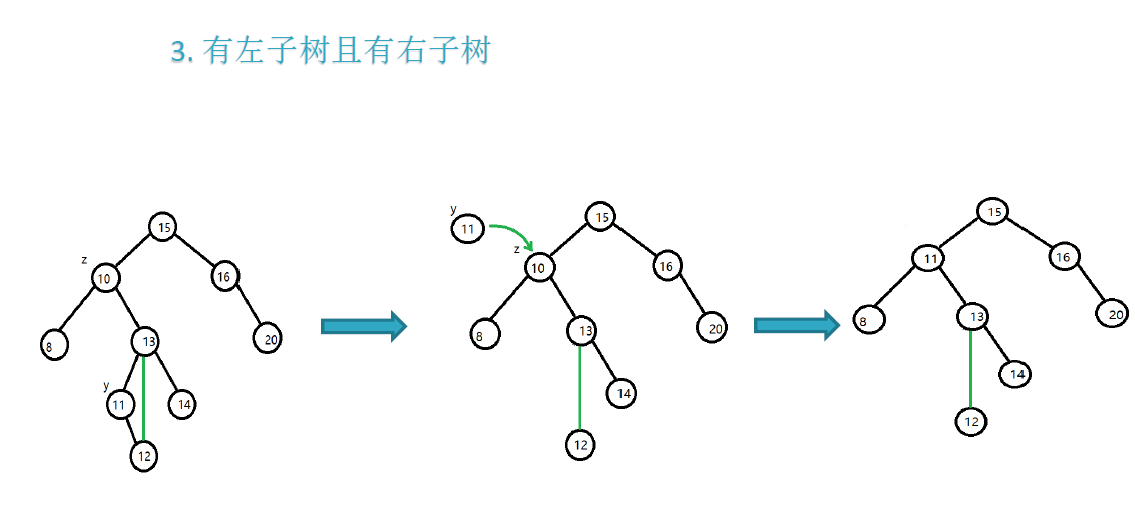
- 代码：

// 5.1 找到node节点的可代替节点，右子树的最小值or左子树的最大值，默认为右子树的最小值
rbtree_node* rbtree_successor(rbtree* T, rbtree_node* node) {
    if (node->right != T->nil) {
        return rbtree_min(T, node->right);
    } else if (node->left != T->nil) {
        return rbtree_max(T, node->left);
    }

    return node;
}


// 5.3 删除
rbtree_node* rbtree_delete(rbtree* T, rbtree_node* node) {
    rbtree_node* del_node = T->nil;    // 真正待删除的节点
    rbtree_node* son_node = T->nil;    // 待删除的节点的子节点

    // 5.3.1 找到需要删除的节点 del_node
    if ((node->left == T->nil) || (node->right == T->nil)) {
        del_node = node;
    } else {
        del_node = rbtree_successor(T, node);
    }

    // 5.3.2 删除 del_node 节点
    if (del_node->left != T->nil) {
        son_node = del_node->left;
    } else if (del_node->right != T->nil) {
        son_node = del_node->right;
    }

    //if (son_node != T->nil) son_node->parent = del_node->parent;
    son_node->parent = del_node->parent;

    if (del_node->parent == T->nil) {
        T->root = son_node;
    } else if (del_node == del_node->parent->left) {
        del_node->parent->left = son_node;
    } else if (del_node == del_node->parent->right) {
        del_node->parent->right = son_node;
    }

    // 5.3.3 用 del_node 节点，覆盖真正待删除的node节点
    if (del_node != node) {
        node->key = del_node->key;
        node->value = del_node->value;
    }

    // 5.3.4 如果正真删除的y节点为红色，则不需要进行调整；如果为黑色，则需要进行调整，以满足红黑树的性质
    if (del_node == BLACK) {
        rbtree_delete_fixup(T, son_node);
    }

    // 5.3.5 返回真正删除的节点
    return del_node;
}

调整：如果真正删除的节点为红色节点，则不需要调整；如果真正删除的节点为黑色节点，则需要调整，以满足红黑树的性质
- 被删除节点为父节点的左子树：
  - 被删除节点的兄弟节点为红色：
    - 删除：476节点
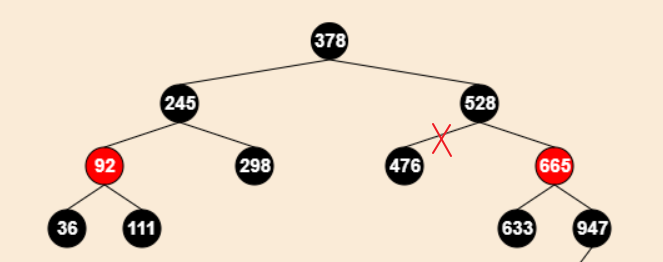
    - 操作：
      - 将兄弟节点设为黑色；
      - 将父节点设为红色；
      - 对父节点进行左旋；
      - 最后，重新设置兄弟节点：bro_node = node→parent→right;
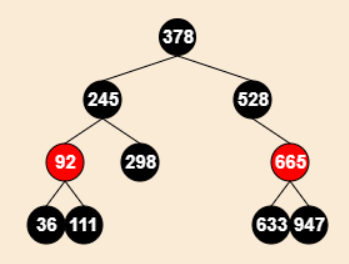
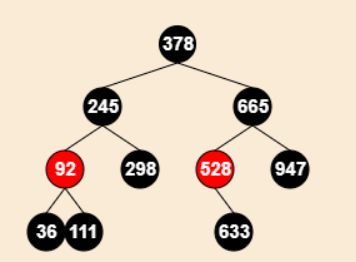
    - 注意：进过以上变换，真正被删除的节点现在是，528节点的左子节点（没有画出来），兄弟节点是633节点，但是这还不是一个红黑树，还需要经过下面的操作；
  - 被删除节点的兄弟节点为黑色：
    - 兄弟节点的左子树为：黑色，右子树为：黑色
      - 接上：真正被删除的节点现在是，528节点的左子节点（没有画出来）
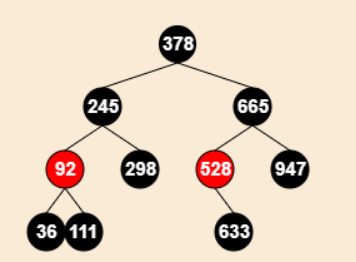
      - 操作：
        
        将被删节点的兄弟节点设为“红色”
        
        设置“被删节点的父节点”为“新的被删节点节点”
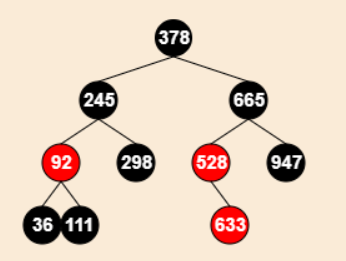
    - 兄弟节点的左子树为：红色，右子树为：黑色
      - 删除：300节点
      - 操作：
        
        将被删节点兄弟节点的左孩子设为“黑色”
        
        将被删节点兄弟节点设为“红色”
        
        对被删节点的兄弟节点进行右旋
        
        右旋后，重新设置被删节点的兄弟节点
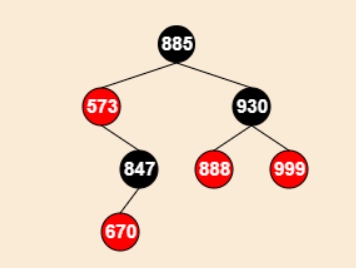
      - 注意：这里的670节点应该为：黑色，标记有误
      - 这时，真正被删除的节点为：573节点的左子节点（未标记出来），兄弟节点为：670节点；还需进行下面的操作
    - 兄弟节点的左子树为：任意，右子树为：红色
      - 接上：
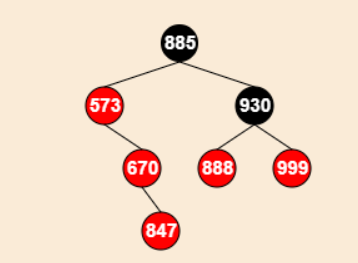
      - 操作：
        
        将被删节点父节点颜色赋值给被删节点的兄弟节点
        
        将被删节点父节点设为“黑色”
        
        将被删节点兄弟节点的右子节点设为“黑色”
        
        对被删节点的父节点进行左旋
        
        设置“被删节点”为“根节点”
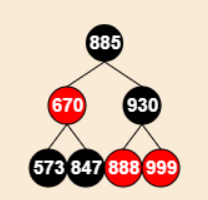
- 被删除节点为**父节点的**右子树：与上基本一样，省略
  - 被删除节点的兄弟节点为红色：
  - 被删除节点的兄弟节点为黑色：
    - 兄弟节点的左子树为：黑色，右子树为：黑色
    - 兄弟节点的左子树为：黑色，右子树为：红色
    - 兄弟节点的左子树为：红意，右子树为：任意

大纲代码：

// 5.2 调整
void rbtree_delete_fixup(rbtree* T, rbtree_node* node) {
    while ((node != T->root) && (node->color == BLACK)) {

        // 1. 删除节点为：左子树
        if (node == node->parent->left) {
            rbtree_node* bro_node = node->parent->right;

            // 1.1 兄弟节点为：红色
            if (bro_node->color == RED) {

            }

            // 1.2 兄弟节点为：黑色
            // 1.2.1 兄弟节点的左子树为：黑色，右子树为：黑色
            if ((bro_node->left->color == BLACK) && (bro_node->right->color == BLACK)) {

            } else {
                // 1.2.2 兄弟节点的左子树为：红色，右子树为：黑色
                if ((bro_node->left->color == RED) && (bro_node->right->color == BLACK)) {

                }

                // 1.2.3 兄弟节点的左子树: 任意，右子树为：红色

            }

        // 2. 删除节点为：右子树
        } else if (node == node->parent->right) {
            rbtree_node* bro_node = node->parent->left;

            // 2.1 兄弟节点为：红色
            if (bro_node->color == RED) {

            }

            // 2.2 兄弟节点为：黑色
            // 2.2.1 兄弟节点的左子树为：黑色，右子树为：黑色
            if ((bro_node->left->color == BLACK) && (bro_node->right->color == BLACK)) {

            } else {
                // 2.2.2 兄弟节点的左子树为：黑色，右子树为：红色
                if ((bro_node->left->color == BLACK) && (bro_node->right->color == RED)) {

                }

                // 2.2.3 兄弟节点的左子树为：红色，右子树为：任意

            }
        }
    }

    node->color = BLACK;
}

完整代码：

// 5.2 调整
void rbtree_delete_fixup(rbtree* T, rbtree_node* node) {
    while ((node != T->root) && (node->color == BLACK)) {

        // 1. 删除节点为：左子树
        if (node == node->parent->left) {
            rbtree_node* bro_node = node->parent->right;

            // 1.1 兄弟节点为：红色
            if (bro_node->color == RED) {
                bro_node->color = BLACK;                // 1. 将兄弟节点设为黑色
                bro_node->parent->color = RED;          // 2. 将父节点设为红色

                rbtree_left_rotation(T, node->parent);  // 3. 对父节点进行左旋
                bro_node = node->parent->right;         // 4. 重新设置兄弟节点
            } 

            // 1.2 兄弟节点为：黑色
            // 1.2.1 兄弟节点的左子树为：黑色，右子树为：黑色
            if ((bro_node->left->color == BLACK) && (bro_node->right->color == BLACK)) {
                bro_node->color = RED; // 1. 将被删节点的兄弟节点设为“红色”
                node = node->parent;   // 2. 设置“被删节点的父节点”为“新的被删节点节点”
            } else {
                // 1.2.2 兄弟节点的左子树为：红色，右子树为：黑色
                if ((bro_node->left->color == RED) && (bro_node->right->color == BLACK)) {
                    bro_node->left->color = BLACK;  // 1. 将被删节点兄弟节点的左孩子设为“黑色”
                    bro_node->color = RED;          // 2. 将被删节点兄弟节点设为“红色”

                    rbtree_right_rotation(T, bro_node);  // 3.对被删节点的兄弟节点进行右旋
                    bro_node = node->parent->right;      // 4.右旋后，重新设置被删节点的兄弟节点
                }

                // 1.2.3 兄弟节点的左子树: 任意，右子树为：红色
                bro_node->color = node->parent->color;  // 1. 将被删节点父节点颜色 赋值给 被删节点的兄弟节点
                node->parent->color = BLACK;            // 2. 将被删节点父节点设为“黑色”
                bro_node->right->color = BLACK;         // 3. 将被删节点兄弟节点的右子节点设为“黑色”
                rbtree_left_rotation(T, node->parent);  // 4. 对被删节点的父节点进行左旋

                node = T->root;                         // 5. 设置“被删节点”为“根节点”
            } 

        // 2. 删除节点为：右子树
        } else if (node == node->parent->right) {
            rbtree_node* bro_node = node->parent->left;

            // 2.1 兄弟节点为：红色
            if (bro_node->color == RED) {
                bro_node->color = BLACK;
                bro_node->parent->color = RED;

                rbtree_right_rotation(T, node->parent);
                bro_node = node->parent->left;
            }

            // 2.2 兄弟节点为：黑色
            // 2.2.1 兄弟节点的左子树为：黑色，右子树为：黑色
            if ((bro_node->left->color == BLACK) && (bro_node->right->color == BLACK)) {
                bro_node->color = RED;
                node = node->parent;
            } else {
                // 2.2.2 兄弟节点的左子树为：黑色，右子树为：红色
                if ((bro_node->left->color == BLACK) && (bro_node->right->color == RED)) {
                    bro_node->right->color = BLACK;
                    bro_node->color = RED;

                    rbtree_left_rotation(T, bro_node);
                    bro_node = node->parent->left;
                }

                // 2.2.3 兄弟节点的左子树为：红色，右子树为：任意
                bro_node->color = node->parent->color;
                node->parent->color = BLACK;
                bro_node->left->color = BLACK;
                rbtree_right_rotation(T, node->parent);

                node = T->root;
            }
        }
    }

    node->color = BLACK;
}

4. 红黑树完整代码

代码：

// 1.2节: 红黑树的实现

#include <stdio.h>
#include <stdlib.h>

#define RED      1
#define BLACK    2

typedef int KEY_TYPE;


// 1. 红黑树的定义
typedef struct _rbtree_node {
    unsigned char color;
    struct _rbtree_node* left;
    struct _rbtree_node* right;
    struct _rbtree_node* parent;

    KEY_TYPE key;
    void* value;
} rbtree_node;

typedef struct {
    rbtree_node* root;
    rbtree_node* nil;
} rbtree;


// 2. 寻找红黑树中的从某个节点开始的的最小节点和最大节点
rbtree_node* rbtree_min(rbtree* T, rbtree_node* node) {  
    if (node == T->nil) return T->nil;

    while (node->left != T->nil) {
        node = node->left;
    }

    return node;
}

rbtree_node* rbtree_max(rbtree* T, rbtree_node* node) {
    if (node == T->nil) return T->nil;

    while (node->right != T->nil) {
        node = node->right;
    }

    return node;
}



// 3. 左旋和右旋
void rbtree_left_rotation(rbtree* T, rbtree_node* x) {
    if (x == T->nil) return;
    rbtree_node* y = x->right;

    if (y == T->nil) return;

    // 3.1 
    x->right = y->left;
    if (y->left != T->nil) {
        y->left->parent = x;
    }

    // 3.2 
    y->parent = x->parent;
    if (x->parent == T->nil) {
        T->root = y;
    } else if (x == x->parent->left) {
        x->parent->left = y;
    } else if (x == x->parent->right) {
        x->parent->right = y;
    }

    // 3.3 
    y->left = x;
    x->parent = y;
}

void rbtree_right_rotation(rbtree* T, rbtree_node* y) {
    if (y == T->nil) return;
    rbtree_node* x = y->left;

    if (x == T->nil) return;

    // 3.1 
    y->left = x->right;
    if (x->right != T->nil) {
        x->right->parent = y;
    }

    // 3.2 
    x->parent = y->parent;
    if (y->parent == T->nil) {
        T->root = x;
    } else if (y == y->parent->left) {
        y->parent->left = x;
    } else if (y == y->parent->right) {
        y->parent->right = x;
    }

    // 3.3
    x->right = y;
    y->parent = x;
}


// 4. 红黑树的插入
void rbtree_insert_fixup(rbtree* T, rbtree_node* node) {
    // 只有父节点也是红色节点的时，才需要调整
    while (node->parent->color == RED) {
        // 4.1 父节点是爷爷节点的左子树
        if (node->parent == node->parent->parent->left) {
            rbtree_node* uncle_node = node->parent->parent->right;

            // 4.1.1 叔父节点是红色节点
            if (uncle_node->color == RED) {
                node->parent->parent->color = RED;
                node->parent->color = BLACK;
                uncle_node->color = BLACK;

                node = node->parent->parent;

            // 4.1.2 叔父节点是黑色节点
            } else if (uncle_node->color == BLACK) {
                if (node == node->parent->right) {
                    node = node->parent;
                    rbtree_left_rotation(T, node);
                }

                node->parent->color = BLACK;
                node->parent->parent->color = RED;
                rbtree_right_rotation(T, node->parent->parent);
            }

        // 4.2 父节点是爷爷节点的右子树
        } else if (node->parent == node->parent->parent->right) {
            rbtree_node* uncle_node = node->parent->parent->left;

            // 4.2.1 叔父节点是红色节点
            if (uncle_node->color == RED) {
                node->parent->parent->color = RED;
                node->parent->color = BLACK;
                uncle_node->color = BLACK;

                node = node->parent->parent;

            // 4.2.2 叔父节点是黑色节点
            } else if (uncle_node->color == BLACK) {
                if (node == node->parent->left) {
                    node = node->parent;
                    rbtree_right_rotation(T, node);
                }

                node->parent->color = BLACK;
                node->parent->parent->color = RED;
                rbtree_left_rotation(T, node->parent->parent);
            }
        }
    }

    T->root->color = BLACK;
}

void rbtree_insert(rbtree* T, rbtree_node* node) {
    // 4.1 找到插入位置的父节点
    rbtree_node* x = T->root;
    rbtree_node* y = T->nil;

    while (x != T->nil) {
        y = x;

        if (node->key == x->key) {
            return;    // 一样，不做处理
        } else if (node->key < x->key) {
            x = x->left;
        } else if (node->key > x->key) {
            x = x->right;
        }
    }

    // 4.2 插入
    node->parent = y;
    if (y == T->nil) {
        T->root = node;
    } else if (y->key > node->key) {
        y->left = node;
    } else if (y->key < node->key) {
        y->right = node;
    }

    node->left = T->nil;
    node->right = T->nil;
    node->color = RED;    // 默认插入红色

    // 4.3 调整
    rbtree_insert_fixup(T, node);
}


// 5. 红黑树的删除
// 5.1 找到node节点的可代替节点，右子树的最小值or左子树的最大值，默认为右子树的最小值
rbtree_node* rbtree_successor(rbtree* T, rbtree_node* node) {
    if (node->right != T->nil) {
        return rbtree_min(T, node->right);
    } else if (node->left != T->nil) {
        return rbtree_max(T, node->left);
    }

    return node;
}

// 5.2 调整
void rbtree_delete_fixup(rbtree* T, rbtree_node* node) {
    while ((node != T->root) && (node->color == BLACK)) {

        // 1. 删除节点为：左子树
        if (node == node->parent->left) {
            rbtree_node* bro_node = node->parent->right;

            // 1.1 兄弟节点为：红色
            if (bro_node->color == RED) {
                bro_node->color = BLACK;
                bro_node->parent->color = RED;

                rbtree_left_rotation(T, node->parent);
                bro_node = node->parent->right;
            }

            // 1.2 兄弟节点为：黑色
            // 1.2.1 兄弟节点的左子树为：黑色，右子树为：黑色
            if ((bro_node->left->color == BLACK) && (bro_node->right->color == BLACK)) {
                bro_node->color = RED;
                node = node->parent;
            } else {
                // 1.2.2 兄弟节点的左子树为：红色，右子树为：黑色
                if ((bro_node->left->color == RED) && (bro_node->right->color == BLACK)) {
                    bro_node->left->color = BLACK;
                    bro_node->color = RED;

                    rbtree_right_rotation(T, bro_node);
                    bro_node = node->parent->right;
                }

                // 1.2.3 兄弟节点的左子树: 任意，右子树为：红色
                bro_node->color = node->parent->color;
                node->parent->color = BLACK;
                bro_node->right->color = BLACK;
                rbtree_left_rotation(T, node->parent);

                node = T->root;
            }

        // 2. 删除节点为：右子树
        } else if (node == node->parent->right) {
            rbtree_node* bro_node = node->parent->left;

            // 2.1 兄弟节点为：红色
            if (bro_node->color == RED) {
                bro_node->color = BLACK;
                bro_node->parent->color = RED;

                rbtree_right_rotation(T, node->parent);
                bro_node = node->parent->left;
            }

            // 2.2 兄弟节点为：黑色
            // 2.2.1 兄弟节点的左子树为：黑色，右子树为：黑色
            if ((bro_node->left->color == BLACK) && (bro_node->right->color == BLACK)) {
                bro_node->color = RED;
                node = node->parent;
            } else {
                // 2.2.2 兄弟节点的左子树为：黑色，右子树为：红色
                if ((bro_node->left->color == BLACK) && (bro_node->right->color == RED)) {
                    bro_node->right->color = BLACK;
                    bro_node->color = RED;

                    rbtree_left_rotation(T, bro_node);
                    bro_node = node->parent->left;
                }

                // 2.2.3 兄弟节点的左子树为：红色，右子树为：任意
                bro_node->color = node->parent->color;
                node->parent->color = BLACK;
                bro_node->left->color = BLACK;
                rbtree_right_rotation(T, node->parent);

                node = T->root;
            }
        }
    }

    node->color = BLACK;
}



// 5.3 删除
rbtree_node* rbtree_delete(rbtree* T, rbtree_node* node) {
    rbtree_node* del_node = T->nil;    // 真正待删除的节点
    rbtree_node* son_node = T->nil;    // 待删除的节点的子树

    // 5.3.1 找到需要删除的节点 del_node
    if ((node->left == T->nil) || (node->right == T->nil)) {
        del_node = node;
    } else {
        del_node = rbtree_successor(T, node);
    }

    // 5.3.2 删除 del_node 节点
    if (del_node->left != T->nil) {
        son_node = del_node->left;
    } else if (del_node->right != T->nil) {
        son_node = del_node->right;
    }

    //if (son_node != T->nil) son_node->parent = del_node->parent;
    son_node->parent = del_node->parent;

    if (del_node->parent == T->nil) {
        T->root = son_node;
    } else if (del_node == del_node->parent->left) {
        del_node->parent->left = son_node;
    } else if (del_node == del_node->parent->right) {
        del_node->parent->right = son_node;
    }

    // 5.3.3 用 del_node 节点，覆盖真正待删除的node节点
    if (del_node != node) {
        node->key = del_node->key;
        node->value = del_node->value;
    }

    // 5.3.4 如果正真删除的y节点为红色，则不需要进行调整；如果为黑色，则需要进行调整，以满足红黑树的性质
    if (del_node->color == BLACK) {
        rbtree_delete_fixup(T, son_node);
    }

    // 5.3.5 返回真正删除的节点
    return del_node;
}



// 6. 红黑树的查找
rbtree_node* rbtree_search(rbtree* T, KEY_TYPE key) {
    rbtree_node* node = T->root;

    while (node != T->nil) {
        if (key == node->key) return node;
        else if (key > node->key) node = node->right;
        else if (key < node->key) node = node->left;
    }

    return T->nil;
}


// 7. 红黑树的遍历
void rbtree_traversal(rbtree* T, rbtree_node* node) {
    if (node != T->nil) {
        rbtree_traversal(T, node->left);
        printf("key: %d, color: %d\n", node->key, node->color);
        rbtree_traversal(T, node->right);
    }
}


// 8. main
int main() {
    int keys[20] = {24,25,13,35,23, 26,67,47,38,98, 20,19,17,49,12, 21,9,18,14,15};

    // 8.1 初始化 T
    rbtree* T = (rbtree*)malloc(sizeof(rbtree));
    if (T == NULL) {
        printf("malloc fail\n");
        return 1;
    }

    T->nil = (rbtree_node*)malloc(sizeof(rbtree_node));
    T->nil->color = BLACK;
    T->root = T->nil;

    // 8.2 插入 node
    for (int i = 0; i < 20; ++i) {
        rbtree_node* node = (rbtree_node*)malloc(sizeof(rbtree_node));
        node->key = keys[i];
        node->value = NULL;

        rbtree_insert(T, node);
    }

    // 8.3 遍历
    rbtree_traversal(T, T->root);

    printf("----------------------------------------\n");

  for (int i = 0; i < 20; ++i) {

    rbtree_node* node = rbtree_search(T, keys[i]);
    rbtree_node* cur = rbtree_delete(T, node);
    free(cur);

    rbtree_traversal(T, T->root);
    printf("----------------------------------------\n");
  }

    return 0;
}

热门文章