奇妙的安全旅行之DSA算法 - HelloWorld开发者社区

hi，大家好，我是开发者FTD。今天我们来介绍一下非对称加密算法中的DSA算法。

DSA 算法简介

DSA（Digital Signature Algorithm）是Schnorr和ElGamal签名算法的变种，被美国NIST作为DSS(DigitalSignature Standard) 数字签名的标准。

DSA是一种更高级的验证方式，它是一种公开密钥算法，不能用来加密数据，一般用于数字签名和认证。DSA 不单单只有公钥、私钥，还有数字签名。私钥加密生成数字签名，公钥验证数据及签名。在DSA数字签名和认证中，发送者使用自己的私钥对文件或消息进行签名，接受者收到消息后使用发送者的公钥来验证签名的真实性，包括数据的完整性以及数据发送者的身份。如果数据和签名不匹配则认为验证失败！数字签名的作用就是校验数据在传输过程中不被修改。

DSA数字签名可以理解为是单向加密的升级，不仅校验数据完整性，还校验发送者身份，同时还由于使用了非对称的密钥来保证密钥的安全，所以相比消息摘要算法更安全。

DSA只是一种算法，和RSA不同之处在于它不能用作加密和解密，也不能进行密钥交换，只用于签名,它比RSA要快很多。

DSA 算法签名过程

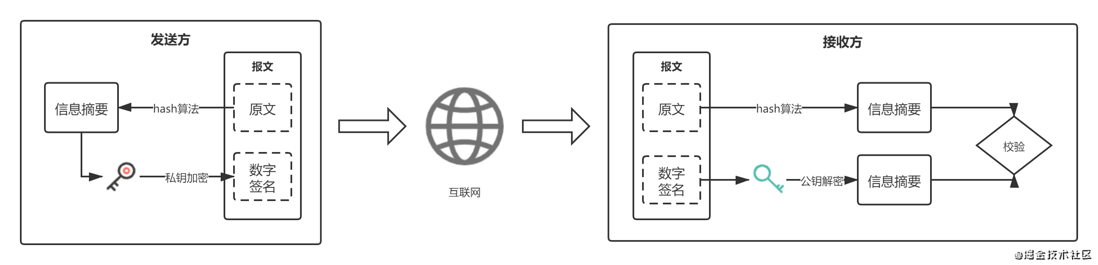
奇妙的安全旅行之DSA算法

使用消息摘要算法将要发送数据加密生成信息摘要。
发送方用自己的DSA私钥对信息摘要再加密，形成数字签名。
将原报文和加密后的数字签名一并通过互联网传给接收方。
接收方用发送方的公钥对数字签名进行解密，同时对收到的数据用消息摘要算法产生同一信息摘要。
将解密后的信息摘要和收到的数据在接收方重新加密产生的摘要进行比对校验，如果两者一致，则说明在传送过程中信息没有破坏和篡改；否则，则说明信息已经失去安全性和保密性。

DSA 算法原理

DSA是基于整数有限域离散对数难题的，其安全性与RSA相比差不多。DSA的一个重要特点是两个素数公开，这样，当使用别人的p和q时，即使不知道私钥，你也能确认它们是否是随机产生的，还是作了手脚。

DSA 算法参数定义

p：一个素模数，其值满足：2^(L-1) < p < 2^L，其中L是64的倍数，且满足512≤ L ≤ 1024
q：(p-1)的素因子，其值满足2^159 < q < 2^160，即q长度为160位。
g：g = powm(h,(p-1)/q,p)。h为满足1 < h < p-1 的任意整数，从而有powm(h,(p-1)/q,p) > 1
x：私钥。x为一个随机或伪随机生成的整数，其值满足 0 < x < q。
y：公钥。y = powm(g,x,p)

注：

整数p，q，g可以公开，也可以仅由一组特定用户共享。
私钥x和公钥y称为一个密钥对(x,y)，私钥只能由签名者本人独自持有，公钥则可以公开发布。密钥对可以在一段时间内持续使用。

DSA 签名过程：

产生一个随机数k，其值满足 0 < k < q
计算r = powm(g,k,p) mod q，其值满足 r > 0
计算 s = (k^(-1)(SHA(M) + x * r)) mod q，其值满足 s > 0

注：

k^(-1) 表示整数k关于某个模数的逆元，并非指k的倒数。k在每次签名时都要重新生成，用于不要将同样的k用于进行其他的签名运算！
- 逆元：满足(a b) mod m = 1 的a 和 b 互为关于模数 m 的逆元，表示为 a = b^(-1) 或 b = a^(-1)。如(2 5) mod 3 = 1,则 2 和 5 互为模数 3 的逆元。
SHA(M)： M 的 hash 值，M为待签名的明文。SHA 是一个单向散列函数。DSS中选用SHA1算法，此时SHA(M) 为160 bits长的数字串，其满足不可逆和抗碰撞性。
最终的签名就是证书对(r, s)，它们和 M 一起发送到验证方。
尽管 r 和 s 为 0 的概率相当小，但只要有任何一个为 0 ，必须重新生成 k，并重新计算 r 和 s 。

DSA 验证签名过程：

我们用(r', s', M') 来表示验证方通过某种途径获得的签名结果，之所以这样表示是因为你不能保证你这个签名的结果一定是发送方生成的真签名相反有可能被人篡改过，甚至掉了包。为了描述简便，下面仍用(r, s, M) 代替(r', s', M')。

为了验证(r, s, M) 的签名是否确由发送方所签，验证方需要有(g, p, q, y)，验证过程如下：

计算 w = s^(-1) mod q
计算 u1 = (SHA(M) * w) mod q
计算 u2 = (r * w) mod q
计算 v = (((g^u1) (y^u2)) mod p ) mod q = ((g^u1 mod p) (y^u2 mod p) mod p) mod q = (powm(g, u1, p) * powm(y, u2, p) mod p) mod q
若 v等于 r，则通过验证，否则验证失败

注：

验证通过说明：签名(r, s) 有效，即(r, s, M) 确为发送方的真实签名结果，真实性可以高度信任，M未被篡改，为有效信息。
验证失败说明：签名(r, s) 无效，即(r, s, M) 不可靠，或者M被篡改过，或者签名是伪造的，或者M的签名有误，M为无效信息。

DSA 算法实现

DSA密钥生成：

public static Map<String, Object> initKey(String seed) throws Exception {
    KeyPairGenerator keygen = KeyPairGenerator.getInstance(KEY_ALGORITHM);
    // 初始化随机产生器   
    SecureRandom secureRandom = new SecureRandom();
    secureRandom.setSeed(seed.getBytes());
    keygen.initialize(1024, secureRandom);

    KeyPair keys = keygen.genKeyPair();

    PublicKey publicKey = keys.getPublic();
    PrivateKey privateKey = keys.getPrivate();

    Map<String, Object> map = new HashMap<String, Object>(2);
    map.put(PUBLIC_KEY, publicKey);
    map.put(PRIVATE_KEY, privateKey);

    return map;
}

用私钥对信息生成数字签名：

public static String sign(byte[] data, String privateKey) throws Exception {
    // 解密由base64编码的私钥   
    byte[] keyBytes = Base64.decodeBase64(privateKey);

    // 构造PKCS8EncodedKeySpec对象   
    PKCS8EncodedKeySpec pkcs8KeySpec = new PKCS8EncodedKeySpec(keyBytes);

    // KEY_ALGORITHM 指定的加密算法   
    KeyFactory keyFactory = KeyFactory.getInstance(KEY_ALGORITHM);

    // 取私钥匙对象   
    PrivateKey priKey = keyFactory.generatePrivate(pkcs8KeySpec);

    // 用私钥对信息生成数字签名   
    Signature signature = Signature.getInstance(SIGNATURE_ALGORITHM);
    signature.initSign(priKey);
    signature.update(data);

    return Base64.encodeBase64String(signature.sign());
}

校验数字签名：

public static boolean verify(byte[] data, String publicKey, String sign)
        throws Exception {

    // 解密由base64编码的公钥   
    byte[] keyBytes = Base64.decodeBase64(publicKey);

    // 构造X509EncodedKeySpec对象   
    X509EncodedKeySpec keySpec = new X509EncodedKeySpec(keyBytes);

    // KEY_ALGORITHM 指定的加密算法   
    KeyFactory keyFactory = KeyFactory.getInstance(KEY_ALGORITHM);

    // 取公钥匙对象   
    PublicKey pubKey = keyFactory.generatePublic(keySpec);

    Signature signature = Signature.getInstance(SIGNATURE_ALGORITHM);
    signature.initVerify(pubKey);
    signature.update(data);

    // 验证签名是否正常   
    return signature.verify(Base64.decodeBase64(sign));
}