SkipList跳表的原理以及Go语言实现

跳表的原理

跳表（Skiplist）是一个特殊的链表，相比一般的链表，有更高的查找效率，可比拟二叉查找树。跳表的查找、插入、删除时间复杂度都是O(logN)。
许多知名的开源软件中的数据结构采用了跳表这种数据结构，例如：

Redis中的有序集合zset
LevelDB、HBase中Memtable
ApacheLucene中的TermDictionary、Posting List

跳表数据结构是由William Pugh发明的，最早出现于他在1990年发表的论文《Skip Lists: A Probabilistic Alternative to Balanced Trees》。跳表本质上是一个链表, 它其实是由有序链表发展而来。跳表在链表之上做了一些优化，跳表在有序链表之上加入了若干层用于索引的有序链表。索引链表的结点来源于基础链表，不过只有部分结点会加入索引链表中，并且越高层的链表结点数越少。跳表查询从顶层链表开始查询，然后逐级展开，直到底层链表。这种查询方式与树结构非常类似，使得跳表的查询效率相近树结构。另外跳表使用概率均衡技术而不是使用强制性均衡，因此对于插入和删除结点比传统上的平衡树算法更为简洁高效。因此跳表适合增删操作比较频繁，并且对查询性能要求比较高的场景。
为了说明跳变的原理以及特点，我们先从有序链表说起。首先看看有序链的特点，并对有序链表的操作性能进行分析。下图是一个有序链表的例子：
SkipList跳表的原理以及Go语言实现
有序链表是一个线性结构，不能像有序数组那样使用二分法查找数据（因为二分查找需要用到中间位置的节点，而链表不能随机访问）。在有序链表中找某个数据，需要从头开始逐个进行比较，直到找到包含数据的那个节点，或者找到第一个比给定数据大的节点为止，时间复杂度为O(n)。当向有序链表中插入数据的时候，也要经历同样的查找过程，从而确定插入位置，因此向链表中插入一个节点的时间复杂度为也是O(n)。

接下来看看跳表是如何改进有序链表从而达到高性能的查询以及操作。首先为基础链表建立一层索引表，索引表只有基础链表结点的1/2。添加了索引表之后的数据结构如下图所示：
SkipList跳表的原理以及Go语言实现
索引表相当于基础链表的目录，查询时首先从索引表开始查找，当遇到比待查数据大的结点时，再从基础链表中查找。由于索引表的结点只有基础链表的1/2，因此需要比较的结点大大减少，从而可以加快查询速度。

利用同样的方式，我们还为基础链表添加第二层索引表，第二层索引表结点的数量是第一层索引表的1/2，添加了第二层索引表之后的数据结构如下图所示：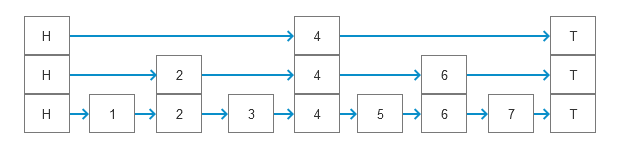
SkipList跳表的原理以及Go语言实现
第二层索引表的结点的数量只有基础链表的1/4左右，查找时首先从第二层索引表开始查找，当遇到比待查数据大的结点时，再从第一层索引表开始查找，然后再从基础链表中查找数据。这种逐层展开的方式与树结构的查询非常类似，因此跳表的查询性能与树结构接近，时间的复杂度为O(logN)。

我们知道一个平衡的二叉树，在进行增加或删除结点后可能造成二叉树结构的不平衡，从而会降低二叉树的查询性能。按照上面的方式实现的跳表也会面临同样的问题，新增或删除结点后会破坏链表之间的比例关系，从而造成跳表查询性能的降低。平衡树通过旋转操作来保持平衡，而旋转一方面增加了代码实现的复杂性，同时也降低了增删操作的性能。真正的跳表不会采用示例中的方式来建立上层链表，而是采用了一种概率均衡技术来创建上层链表，并保证各层链表之间的比例关系。在为跳表增加一个结点时，会调用一个概率函数来计算一个结点的层次（level），例如若level=3，则结点除了出现在基础链表外，还会出现在第一层索引以及第二层索引链表中。结点层次的计算逻辑如下：

每个节点肯定都在基础链表中。
如果一个节点存在于第i层链表，那么它有第(i+1)层链表的概率为p。
节点最大的层数不允许超过一个最大值。

跳表每一个节点的层数是随机的，而且新插入一个节点不会影响其它节点的层数。因此插入操作只需要修改插入节点前后的指针，而不需要对很多节点都进行调整,这就降低了插入操作的复杂度。实际上这是跳表的一个很重要的特性，这让跳表在增删操作的性能上明显优于平衡树的方案。

用Go语言实现跳表

接下来我们给出跳表的Go语言的实现，目前代码已经上传到github中，下载地址

定义

首先给出链接结点的定义：

type SkipNodeInt struct {
   key       int64
   value  interface{}
   next   []*SkipNodeInt
}

其中：

key用于表示一个结点，查询是使用key来查询一个结点。
Val是interface{}类型，可以表示任何类型的数据。
next是各层的后向结点指针数组，数组的长度为层高：level

接下来是链表的结构定义：

type SkipListInt struct {
   SkipNodeInt
   mutex      sync.RWMutex
   update     []*SkipNodeInt
   maxl   int
   skip   int
   level      int
   length     int32
}

其中：

SkipNodeInt 用于代表列表的header。
update:用于查找过程中的临时变量，定义唉这里为了提高访问性能，减少频繁创建数组对象。
maxl：是最大层数，缺省为：32
skip：层之间的比例，例如skip=4，则1/4的结点出现在上层。
level：跳表当前的层数
length：跳表的结点数量

跳表对象的创建：

func NewSkipListInt(skip ...int) *SkipListInt {
    list := &SkipListInt{}
    list.maxl = 32
    list.skip = 4
    list.level = 0
    list.length = 0
    list.SkipNodeInt.next = make([]*SkipNodeInt, list.maxl)
    list.update = make([]*SkipNodeInt, list.maxl)
    if len(skip) == 1 && skip[0] > 1 {
        list.skip = skip[0]
    }
    return list
}

说明：

跳表最大层数缺省为：32
跳表两层之间的比例为1/4，即概率p=0.25
创建跳表是可以指定一个比例参数skip

跳表的查询

查找就是给定一个key，查找这个key是否出现在跳跃表中，如果出现，则返回其值，如果不存在，则返回nil。
查找某个元素时，先从顶层链表中查修，当遇到比待查数据大的结点时，则从下一层链表中查询。当遍历进行到第1层时，下一个节点就是目标节点(如存在)。

func (list *SkipListInt) Get(key int64) interface{} {
    list.mutex.Lock()
    defer list.mutex.Unlock()

    var prev = &list.SkipNodeInt
    var next *SkipNodeInt
    for i := list.level-1; i >= 0; i-- {
        next = prev.next[i]
        for next != nil && next.key < key {
            prev = next
            next = prev.next[i]
        }
    }

    if next != nil && next.key == key {
        return next.value
    } else {
        return nil
    }
}

新增结点

跳表新增结点包含如下几个操作：

查找到需要插入的位置，需要获取每层的前驱节点。
构造新节点，并通过概率函数计算结点的层数：level。
将新节点插入到第0层到第(level-1)层的链表中。

func (list *SkipListInt) Set(key int64, val interface{}) {
    list.mutex.Lock()
    defer list.mutex.Unlock()
    
    //获取每层的前驱节点=>list.update
    var prev = &list.SkipNodeInt
    var next *SkipNodeInt
    for i := list.level-1; i >= 0; i-- {
        next = prev.next[i]
        for next != nil && next.key < key {
            prev = next
            next = prev.next[i]
        }
        list.update[i] = prev
    }

    //如果key已经存在
    if next != nil && next.key == key {
        next.value = val
        return
    }

    //随机生成新结点的层数
    level := list.randomLevel();
    if level > list.level {
        level = list.level + 1;
        list.level = level
        list.update[list.level-1] = &list.SkipNodeInt
    }

    //申请新的结点
    node:= &SkipNodeInt{}
    node.key = key
    node.value = val
    node.next = make([]*SkipNodeInt, level)

    //调整next指向
    for i := 0; i < level; i++ {
        node.next[i] = list.update[i].next[i]
        list.update[i].next[i] = node
    }

    list.length++
}

删除结点

删除操作与添加结点类似，包含以下步骤：

获取每层的前驱节点。

调整指针。

func (list *SkipListInt) Remove(key int64) interface{} {
  list.mutex.Lock()
  defer list.mutex.Unlock()

  //获取每层的前驱节点=>list.update
  var prev = &list.SkipNodeInt
  var next *SkipNodeInt
  for i := list.level-1; i >= 0; i-- {
      next = prev.next[i]
      for next != nil && next.key < key {
          prev = next
          next = prev.next[i]
      }
      list.update[i] = prev
  }

  //结点不存在
  node := next
  if next == nil || next.key != key {
      return nil
  }

  //调整next指向
  for i, v := range node.next {
      if list.update[i].next[i] == node {
          list.update[i].next[i] = v
          if list.SkipNodeInt.next[i] == nil {
              list.level -= 1
          }
      }
      list.update[i] = nil
  }

  list.length--
  return node.value
}

随机层数的生成

随机层数的生成逻辑为：给定一个比例因此P=list.skip，对于i层的节点，有1/P的概率会出现在i+1层。

func (list *SkipListInt) randomLevel() int {
    i := 1
    for ; i < list.maxl; i++ {
        if rand.Int() % list.skip != 0 {
            break
        }
    }
    return i
}

跳表的原理

用Go语言实现跳表

定义

跳表的查询

新增结点

删除结点

随机层数的生成

Andriod第三方源码分析

Android进阶之旅-(Framework源码分析)

热门文章