如有错误,还请指正。
微信扫描下方二维码,一起学习更多计算机基础知识。

9.0. 什么是排序?
排序在日常生活中无处不在。比如考试成绩的排名、体育课的从低到高的队形、网购时按价格升序排列或降序排列等等。
| 姓名 | 学号 | 班级 | 成绩 |
|---|---|---|---|
| 张三 | 1001 | 2班 | 100 |
| 李四 | 1003 | 1班 | 90 |
| 王五 | 1000 | 3班 | 80 |
| 赵六 | 1006 | 2班 | 70 |
在该表格中,我们称一行数据为一条记录,其中姓名、学号等数据项是关键字,关键字是我们排序的依据。关键字可以是主关键字或次关键字,甚至是若干数据项的组合。
比如,在该表格中,我们是按照成绩(次关键字)从高到低降序排序的。也可以按照学号排序,或者按照学号和成绩同时排序:先按成绩降序排列,成绩相同的,按照学号升序排列。
所以,对多条记录排序的本质是对关键字的排序,如果排序依据是多个关键字,可以转化为单个关键字的排序。
所谓排序,是指按指定的关键字,将某个序列的所有元素以有序的方式排列起来。
如何实现排序呢?
比如上体育课时按身高的排序,就是比较两个人的身高,然后矮的站前面,高的站后面。如果高的在前,矮的在后,就交换位置;否则就用不动。
没错,排序是借助比较和交换来实现的。比较的是关键字,这是我们排序的依据。交换的是两个元素的位置,通常我们不真的交换位置,而是借助中间变量的赋值来实现交换位置的效果。
/*一个交换函数,交换数组中下标为i和j的元素位置*/
void swap(int *array, int i, int j)
{
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}在实现排序算法时,我们应当追求更少次数的比较和交换,这样才能提高算法的性能。
为了后面说明问题方便起见,这里约定几个规则:
- 只对数组排序,并约定数组长度
length = 10 - 全部排序算法均按升序排序
- 由于是针对数组,所以关键字就是其元素值本身。比较关键字即是比较元素值,不再区分。
9.1. 暴力排序(Violent Sort)
所谓暴力,是指没有任何技巧而言的方式,它直接粗暴地遍历真个数组,从而不停的进行比较和交换。这是最容易理解的排序算法。
核心思想:从数组的第一个元素开始,将每个元素作为基准元素,基准元素和其后面的所有元素比较,如果基准元素大于其后的某个元素,则与其交换位置;否则位置不变。
当基准元素和其后的所有元素比较交换完后,最小值一定被排好了,此时就说一轮排序完成了,每轮排序有若干次循环,用于比较和交换。像这样进行若干轮的排序后,排序就完成了。
我们需要两个变量,用于标记两个进行比较的元素下标:
- 变量
i:某个元素的下标; - 变量
j:下标i之后的下标。
我们需要两个嵌套循环:
- 外层循环控制轮数;
- 内层循环控制每轮的比较和交换。
动态过程如下:

代码实现如下:
/* 暴力排序
* array : 数组
* length : 数组长度
*/
void violent_sort(int *array, int length)
{
int i, j;
// 外层循环,遍历数组,控制轮数
for (i = 0; i < length; i++) {
// 内层循环,循环比较 array[i] 和其之后的元素,控制循环次数
for (j = i + 1; j < length; j++) {
if (array[i] > array[j]) { // 如果大于则交换
swap(array, i, j);
}
}
}
}通过以上的暴力排序,我们能够初体会排序的思想,即不断地比较和交换。
暴力排序有其明显的缺点,即每个元素都要和其之后的所有的元素比较,这就很容易破坏整个数组的原来顺序,比如在上面的动态过程中,元素 40 在某次交换后被交换到了更靠后的位置。为了排好某个元素,而对其之后的所有元素大动干戈,甚至破坏了它们原来之间的顺序,这就影响了效率。
9.2. 冒泡排序(Bubble Sort)
冒泡排序是一种很简单的排序算法,由暴力排序改进而来。
核心思想:比较相邻的两个元素,当前者大于后者时,交换二者位置;否则位置不变。
注意:冒泡排序是相邻的两个元素比较并交换,而暴力排序是某个元素和其之后的所有元素比较并交换。
当数组中所有的相邻元素进行两两比较和交换后,一定会找到一个最大值,并且最大值被交换到数组尾处,此时说一轮排序完成了,一轮排序中有若干次循环,用于比较和交换。像这样进行若干轮排序后,排序就完成了。
我们需要两个变量:
变量
i:用于控制轮数;变量
j:元素下标,j+1为其相邻元素的下标。
我们需要两个嵌套循环:
- 外层循环控制轮数
- 内层循环控制每轮所有相邻元素的比较和交换
动态过程如下:

代码实现如下:
/* 冒泡排序
* array : 数组
* length : 数组长度
*/
void bubble_sort(int *array, int length)
{
int i, j;
// 外层循环,控制轮数。每一轮排好一个元素
for (i = 0; i < length; i++) {
// 内层循环,循环比较数组中未排序的元素
for (j = 0; j < length - i - 1; j++) {
// 若前者大于后者则交换
if (array[j] > array[j + 1]) {
swap(array, j, j + 1);
}
}
}
}由于是相邻的两个元素进行比较,所以一轮比较后,一定有一个最大的元素被交换到最右边,像“大泡泡”浮到水面上一样,所以我们称其为“冒泡排序”。
冒泡排序虽然改善了暴力排序的缺点,但仍然具有可优化的地方。
在上述动态过程中,第 7 轮(i = 6)时就已经完成排序了,但后面仍然进行了 3 轮的比较。这最后 3 轮是完全没必要的,所以我们可以改进一下,避免没必要的比较。
方法就是增加一个标志变量 unsorted,用于标志数组是否已经有序,unsorted = 0 时数组有序,unsorted = 1 时数组无序。
unsorted 通过记录在某轮排序中是否发生了交换,如果没发生,就意味着已经有序。
void bubble_sort_v3(int *array, int length)
{
int i, j;
int unsorted = 1; // 标识变量
for (i = 0; i < length && unsorted; i++) {
unsorted = 0;
for (j = 0; j < length - i - 1; j++) {
if (array[j] > array[j + 1]) {
swap(array, j, j + 1);
unsorted = 1; // 发生交换,说明尚未有序
}
}
}
}虽然冒泡排序可以避免一些不必要的比较和交换,但是冒泡排序本质仍和暴力排序相似,即不断地大量交换,或是某个元素和其后所有元素的交换,或是两个相邻元素的交换。通过动图也可以看出,要使一个元素排到其正确的位置上,我们往往需要和多个元素相交换,这是影响效率的“硬伤”。
9.3. 简单选择排序(Simple Selection Sort)
简单选择排序则“医治”了上面提到的暴力排序和冒泡排序的“硬伤”。
核心思想:从数组的第一个元素开始,将其作为基准元素,然后找出基准元素之后所有元素中最小的那个,如果这个最小的元素小于基准元素,则交换二者;否则不用交换。
像这样,通过若干次比较和一次交换,最小值一定被排好了,此时说一轮排序完成了,经过若干轮的排序后,排序就完成了。
我们需要三个变量:
- 变量
i:基准元素的下标; - 变量
j:基准元素之后的元素的下标; - 变量
min:找到的最小元素的下标。
需要两个嵌套循环:
- 外层循环用于控制轮数;
- 内层循环用于控制每轮的若干次比较和最多一次的交换。
动态过程如下:

暴力排序和冒泡排序更像是“没脑子”的交换排序,就是说,在该轮排序结束前,我们并不知道最大值或最小值是谁,所以只能靠遍历,边比较边交换该轮的所有元素,等到该轮排序结束后,自然就排好一个元素了。通常表现为一轮排序中有若干次比较、若干次交换。
而简单选择排序则是“有脑子”的排序,就是说,我们在交换前,先比较该轮的所有元素,(如果)找到最小的那个元素,直接将其交换到它该待的位置。通常表现为一轮排序中有若干次比较、最多一次交换。
代码实现如下:
/*
* 简单选择排序
* array : 数组
* length : 数组长度
*/
void simple_selection_sort(int *array, int length)
{
int i, j, min;
for (int i = 0; i < length - 1; i++) {
min = i; // 最小元素初始化为基准元素
// 找最小元素
for (int j = i + 1; j < length; j++) {
if (array[min] > array[j]) {
min = j;
}
}
// 在基准元素之后的元素中找到了比基准元素小的值
if (i != min) {
swap(array, i, min); // 交换
}
}
}9.4. 直接插入排序(Straight Insertion Sort)
我们可以用另一种视角来看待排序,即将一个待排序的数组看成两个部分:有序区和乱序区。
在排序开始前,整个数组都是乱序区,而有序区则为空:
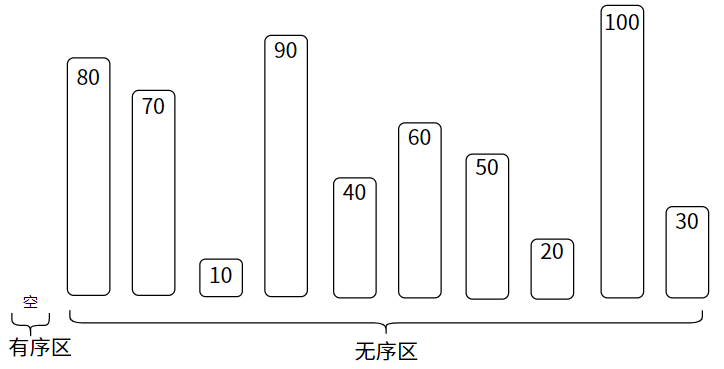
排序开始后,有序区逐渐扩大,乱序区逐渐缩小:
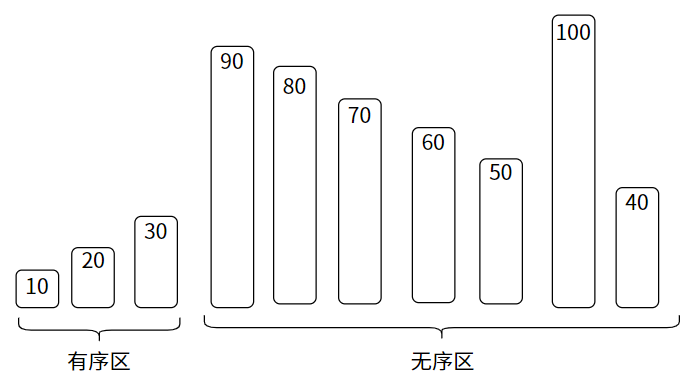
排序完成后,整个数组都是有序区,乱序区则为空:
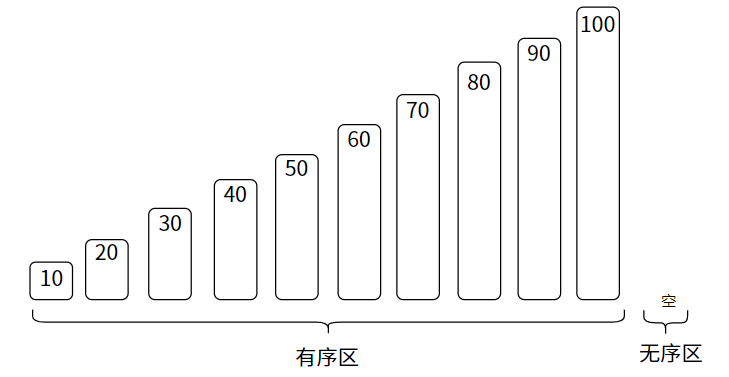
核心思想:将数组看作无序区和有序区两个区,从无序区中选出一个元素,按大小插入到有序区的合适位置。当无序区为空时,有序区自然就完成排序了。
动态过程如下:

代码实现如下:
/*
* 直接插入排序
* array : 数组
* length : 数组长度
*/
void straight_insertion_sort(int *array, int length)
{
int i, j;
// 外层循环 决定待插入值
for (i = 1; i < length; i++) {
if (array[i] < array[i - 1]) {
int tmp = array[i]; // 待插入值
// 内层循环 在有序区中为待插入值腾出位置
for (j = i - 1; j >= 0 && array[j] > tmp; j--) {
array[j + 1] = array[j];
}
array[j + 1] = tmp; // 插入
}
}
}请注意插入元素到有序区的关键代码 array[j + 1] = tmp;中的 j+1。

