完整示例代码请移步至GitHub | Gitee

如有错误，还请指正。

微信扫描下方二维码，一起学习更多计算机基础知识。

2.0. 线性表的链式存储结构

在 1.0 什么是线性表？ 中我们介绍了一种“用曲线连接”的线性表，“曲线”是一种形象化的语言，实际上并不会存在所谓“曲线”的这种东西。

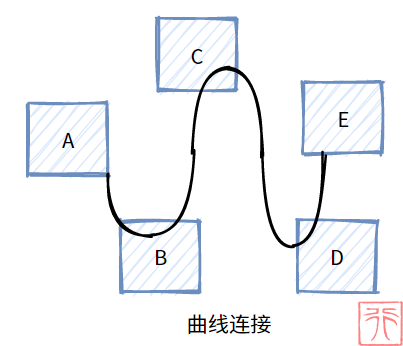
所谓“曲线连接”即链式存储，那什么是链式存储呢？

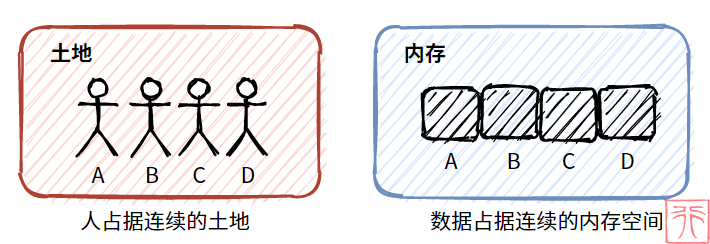
在1.1. 线性表的顺序存储方式中介绍顺序存储结构时举了一个例子：

比如，一群孩子肩并肩地站成一排，占据一定的连续土地。这群孩子的队伍非常整齐划一。

这个例子反映在内存中，即为顺序存储结构。

现在孩子们觉得肩并肩站队太过于约束，于是便散开了，想站在哪里就站在哪里，但是队伍不能中断啊。所以他们便手拉着手来保持队伍不断开。

现在孩子们占据的不是连续的土地了，而是任意的某块土地。

这个例子反映在内存中，就是数据元素任意出现，占据某块内存。

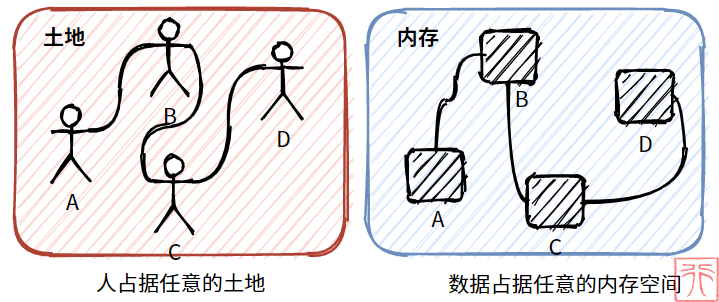
上面两张图放在一块对比，就可以看出问题了：

• 直线 VS 曲线
• 整齐划一 VS 杂乱无章
• 连续内存空间 VS 任意内存空间
• 顺序存储 VS 链式存储

在1.1. 线性表的顺序存储方式中提到过，线性表的特点之一是元素之间有顺序。顺序存储结构靠连续的内存空间来实现这种“顺序”，但链式存储结构的元素是“任意的”，如何实现“顺序”呢？

“任意”和“顺序”乍一看很像反义词，但并不矛盾。小孩子们为了不让队伍中断便“手拉手”，我们要实现“顺序”，就靠那根“像链条一样的曲线”来把元素链接起来，这样就有了顺序。

这就是链式存储。

在1.1. 线性表的顺序存储方式中提到过“顺序存储结构是使用一段连续的内存单元分别存储线性表中的数据的数据结构”。我们照猫画虎，就可以得到“链式存储结构是使用一组任意的、不连续的内存单元来分别存储线性表中的数据的数据结构”的结论。

就使用连续的内存单元来存数据，可不可以？

这就好比，某两个情同手足的兄弟不愿分开，手拉手的肩并肩站着，可不可以？

当然可以！

下图直观地画出了线性表的元素以链式存储的方式存储在内存中。

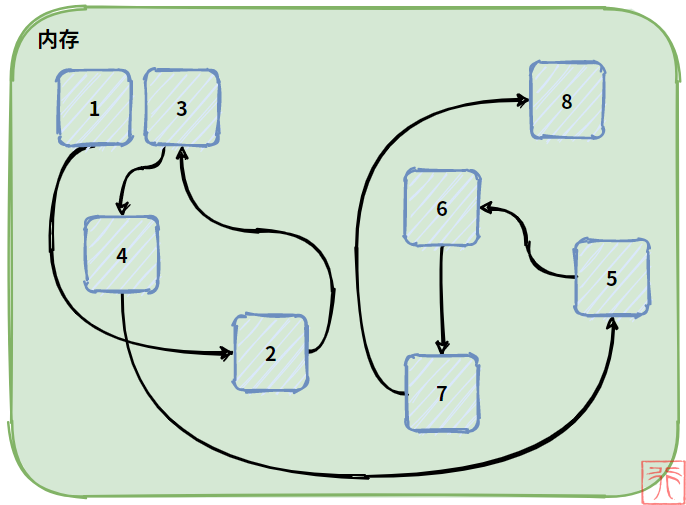
为了方便画图，我们将表示顺序的曲线人为地拉直，将任意存储的元素人为地排列整齐，形成下图中的逻辑关系：

这种链式存储结构的线性表，简称为链表。

上图的链表之间用一个单向箭头相连，从一个指向另一个，这样整个链表就有了一个方向，我们称之为单链表。

总结一下特点：

1. 用一组任意的存储单元来存储线性表的数据元素，这组存储单元可以是连续的（1和3），也可以是不连续的；
2. 这组任意的存储单元用“一根链子”串起来，所以虽然在内存上是乱序的，但是在逻辑上却仍然是线性的；
3. 单链表的方向是单向的，只能从前往后，不能从后往前；

2.1. 单链表的实现思路

因为单链表是任意的内存位置，所以数组肯定不能用了。

因为要存储一个值，所以直接用变量就行。

因为单链表在物理内存上是任意存储的，所以表示顺序的箭头（小孩子的手臂）必须要用代码实现出来。

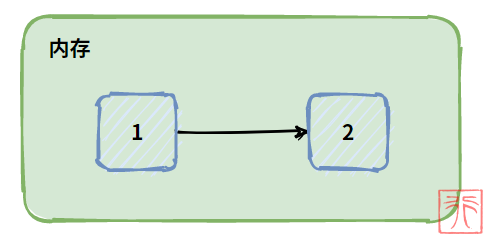
而箭头的含义就是，通过 1 能找到 2。

又因为我们使用变量来存储值，所以，换句话说，我们要通过一个变量找到另一个变量。

变量找变量？怎么做到？

C 语言刚好有这个机制——指针。如果你对指针还不清楚，可以移步到这篇文章——如何掌握 C 语言的一大利器——指针？。

现在万事俱备，只差结合。

一个变量用来存值，一个指针用来存其直接后继的地址，把变量和指针绑在一块构成一个数据元素，啪的一下，就成了。

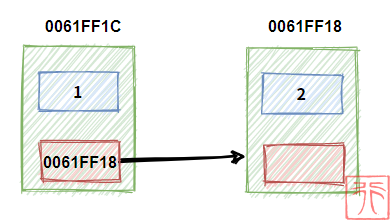
由于指针中存了其直接后继的地址，这就相当于用一个有向箭头指向了其直接后继。

先明确几个名词：

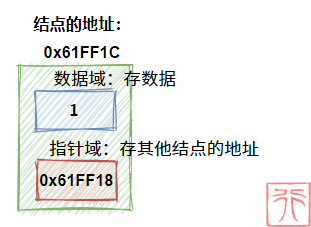
• 用来存数据的变量叫做数据域
• 用来存“直接后继元素的地址”的 指针 叫做指针域
• 数据域和指针域构成的数据元素叫做 结点 (node)

总结一下，一个单链表 (SinglyLinkedList) 的结点 (node) 由以下几部分组成：

• 用来存数据的数据域——data
• 用来存直接后继结点的的地址的指针域——next

2.2. 结点的具体实现

可以使用 C 语言的结构体来实现结点：

为了说明问题简单，我们这里的结点只存储整数。

//结点
typedef struct Node {
    int data; //数据域：存储数据
    struct Node *next; //指针域：存储直接后继结点的地址
} Node;

这样的一个结构体就能完美地表示一个结点了，许多结点连在一块就能构成链表了。

2.3. 单链表的结构

单链表由若干的结点单向链接组成，一个单链表必须要有头有尾，因为计算机很“笨”，不像人看一眼就知道头在哪尾在哪。所以我们要用代码清晰地表示出一个单链表的所有结构。

2.3.0. 头指针

请先注意 “头” 这个概念，我们在日常生活中拿绳子的时候，总喜欢找“绳子头”，此“头”即彼“头”。

然后再理解 “指针” 这个概念（如不清楚指针，请移步至该文章），指针里面存储的是地址。

那么，头指针即存储链表的第一个结点的内存地址的指针，也即头指针指向链表的第一个结点。

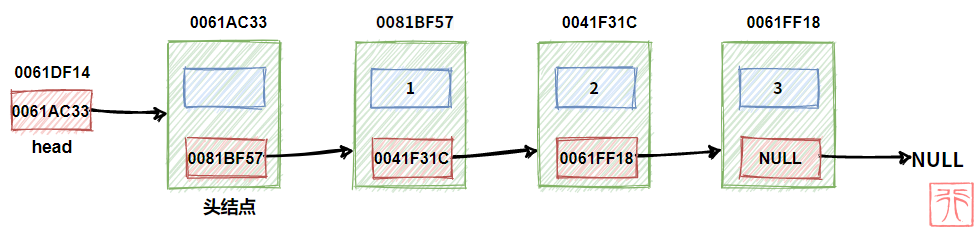
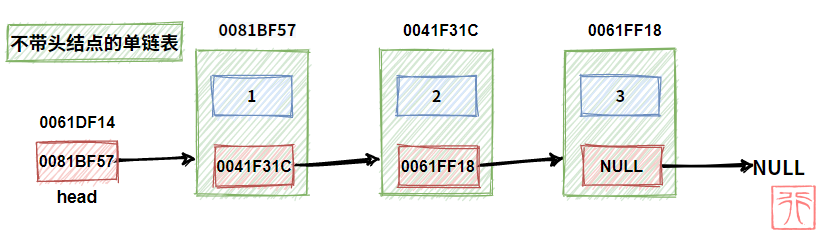
下图是一个由三个结点构成的单链表：

（为了方便理解链表的结构，我会给出每个结点的地址以及指针域的值）

指针 head 中保存了第一个结点 1 的地址，head 即为头指针。有了头指针，我们就可以找到第一个结点的位置，就可以找到整个链表。通常，头指针的名字就是链表的名字。

即，head（头指针）在手，链表我有。

值为 3 的结点是该链表的“尾”，所以它的指针域中保存的值为 NULL，用来表示整个链表到此为止。

我们用头指针表示链表的开始，用 NULL 表示链表的结束。

2.3.1. 头结点

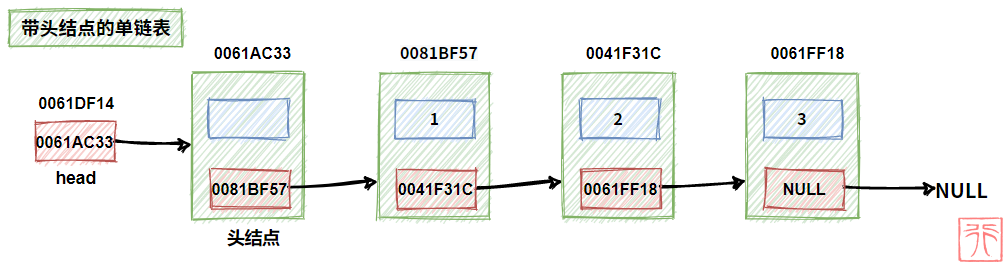
在上面的链表中，我们可以在值为 1 的结点前再加一个结点，称其为头结点。见下图：

头结点的指针域中一般不存放数据（可以存放如结点数等无关紧要的数据），从这点看，头结点是不同于其他结点的“假结点”。

此时头指针指向头结点，因为现在头结点才是第一个结点。

为什么要设立头结点呢？这可以方便我们对链表的操作，后面你将会体会到这一点。

当然，头结点不是链表的必要结构之一，他可有可无，仅凭你的喜好。

2.3.2. 有无头结点的单链表

既然头结点不是链表的必要结构，这就意味着可以有两种链表：

• 带头结点的单链表
• 不带头结点的单链表

再加上头指针，初学链表时，“我们的头”很容易被“链表的头”搞晕。

别晕，看下面通过两幅图：

记住以下几条：

• 头指针很重要，没它不行。
• 虽然头结点可以方便我们的一些操作，但是有没有都行。
• 无论带头结点与否，头指针都指向链表的第一个结点。

（后面的操作我们将讨论不带头结点和带头结点两种情况）

2.4. 空链表

【不带头结点】

下图是一个不带头结点的空链表：

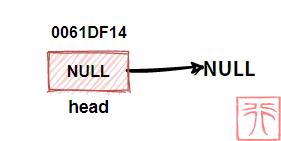
即头指针中存储的地址为 NULL。

【带头结点】

下图是一个带头结点的空链表：

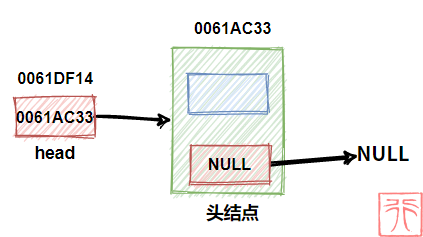
此时头指针中存储的是第一个结点——头结点的地址，头结点的指针域中存储的是 NULL 。

（后面的图示将不再给出内存地址）

2.5. 创造结点

至此，关于单链表的基本概念、实现思路、结点的具体实现我们都已经了解了，但这些还都停留我们的脑子里。下面要做的就是把我们脑子里的东西，以内存喜闻乐见的形式搬到内存中去。

因为链表是由结点组成的，所以我们先来创造结点。

/**
 * 创造结点，返回指向该结点的指针
 * elem : 结点的数据域的值
 * return : 指向该结点的指针（该结点的地址）
 */
Node *create_node(int elem)
{
    Node *node = (Node *) malloc(sizeof(Node));
    node->data = elem;
    node->next = NULL;
    return node;
}

注意：我们要使用 malloc 函数给结点申请一块内存，然后才能对该结点的数据域进行赋值，而由于该结点此时是一个独立的结点，没有直接后继结点，所以其指针域为 NULL。

2.6. 初始化链表

初始化链表即初始化一个空链表，然后才能在空链表的基础上进行操作，详见 【2.4. 空链表】中的两幅图。

【不带头结点】

要初始化一个不带头节点的链表，我们直接创建一个可以指向结点的空指针即可，该空指针即为头指针：

Node *head = NULL;

【带头结点】

带头结点的单链表的特点是多了一个不存储数据的头结点，所以我们初始化链表时，要将其创建出来。

但是在创建之前，我们先来搞清楚三个问题，分别是：

1. 链表的头指针

2. 指向【指向结点的指针】的指针

3. 函数参数的值传递和地址传递

简单解释：

1. 头指针是链表一定要有的，找到头指针才能找到整个链表，否则整个链表就消失在“茫茫内存”之中了。所以无论进行何种操作，头指针一定要像我们攥紧绳子头一样被“攥”在我们手中。
2. 指针中保存了别人的地址，但它也有自己地址。如果一个指针中保存了别的指针的地址，该指针就是“指向指针的指针”。因为头指针是指向链表第一个结点的指针，所以我们找到头指针也就找到了整个链表（这句话啰嗦太多遍了）。而为了能找到头指针，我们就需要知道头指针的地址，也即将头指针的地址保存下来，换句话说，用一个指针来指向头指针。
3. 函数的值传递改变的是形参（实参的一份拷贝），影响不了实参。所以在一些情况下，我们需要传给函数的是地址，函数使用指针来直接操作该指针指向的内存。

如果以上内容还不清楚，说明对指针的掌握还不够熟练，请移步至文章【如何掌握 C 语言的一大利器——指针？】。

下面画一张比较形象的图：

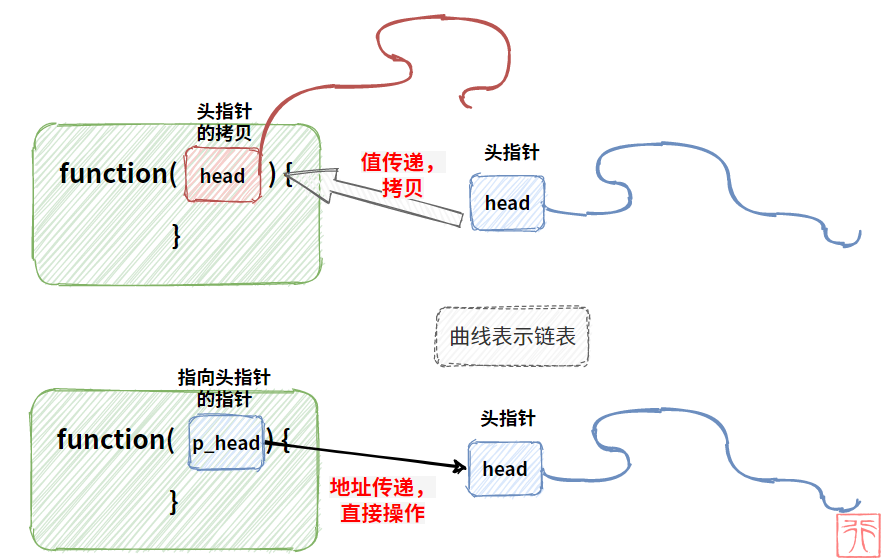
上图中头指针和链表像不像一根带棍子的鞭子？比如下面这个我小时候经常玩的游戏

把链表比作打陀螺的鞭子，头指针比作鞭子头，指向头指针的指针则像攥在手中的那根棍子一样。

/**
 * 初始化链表
 * p_head: 指向头指针的指针
 */
void init(Node **p_head)
{
    //创建头结点
    Node *node = (Node *) malloc(sizeof(Node));
    node->next = NULL;
    //头指针指向头结点
    *p_head = node;
}

2.7. 遍历操作

所谓遍历，就是从链表头开始，向链表尾一个一个结点进行遍历，我们通常借助一个辅助指针来进行遍历。

【不带头结点】

不带头结点的链表从头指针开始遍历，所以辅助指针的初始位置就是头指针，这里我们以获取链表的长度为例：

int get_length(Node *head)
{
    int length = 0;
    Node *p = head;
    while (p != NULL) {
        length++;
        p = p->next;
    }
    return length;
}

使用 for 循环能使代码看起来更精简些。

【带头结点】

带头结点的链表需要从头结点开始遍历，所以辅助指针的初始位置是头结点的后继结点：

int get_length(Node *head)
{
    int length = 0;
    Node *p = head->next;
    while (p != NULL) {
        length++;
        p = p->next;
    }
    return length;
}

2.7. 插入操作

2.7.0. 基本思想

我们在前面举了“小孩子手拉手”这个例子来描述单链表。

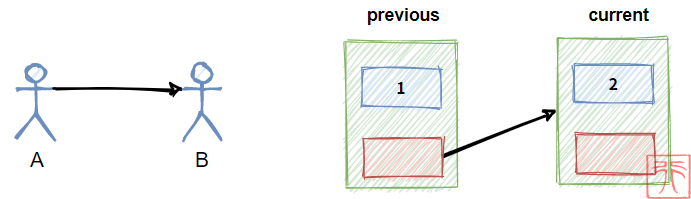
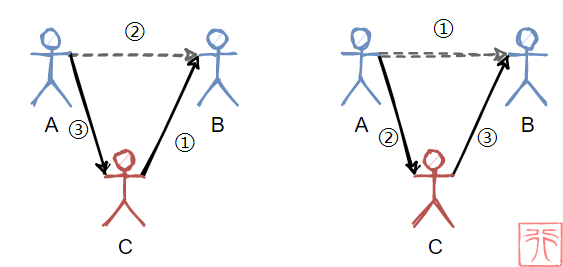
孩子 A 和 B 手拉手链接在一起，现在有个孩子 C 想要插到他们之间，怎么做？

C 拉上 B 的手 => A 松开 B 的手（虚线表示松开） => A 拉上 C 的手

A 松开 B 的手 => A 拉上 C 的手 => C 拉上 B 的手

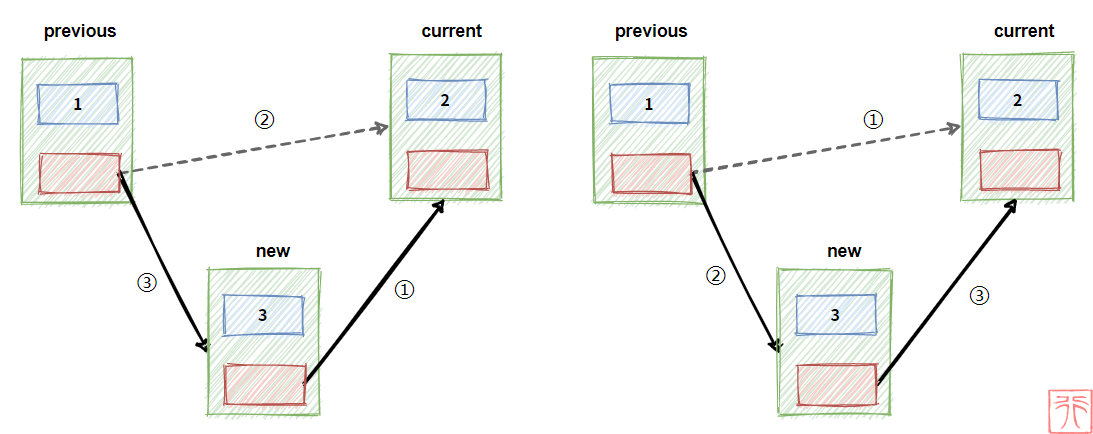
同样地，在链表中，我们也是类似的操作：

写成代码就是：

new->next = current;
previous->next = new;

或这换一下顺序：

previous->next = new;
new->next = current;

这两句就是插入操作的核心代码，也是各种情况下插入操作的不变之处，搞明白这两句，就可以以不变应万变了。

其中 previous 、 current 和 new 是三个指向结点的指针， new 指向要插入的结点， previous 、 current 一前一后，在进行插入操作之前的关系为：

current = previous->next;

事实上， current 指针不是必需的，只有一个 previous 也可以做到插入操作，原因就是 current = previous->next，这种情况下的核心代码变为：

new->next = previous->next;
previous->next = new;

但请注意，在这种情况下两句代码是有顺序的，你不能写成：

// 错误代码
previous->next = new;
new->next = previous->next;

我们可以从两个角度来理解为什么这两句会有顺序：

【角度一】

因为 current 指针的作用就是用来保存 previous 的直接后继结点的地址的，所以在我们断开 previous 和 current 联系后，我们仍能找到 current 及其以后的结点。“链子”就算暂时断开了，由于断开处两侧都有标记，我们也能接上去。。

但是现在没了 current 之后，一旦断开， current 及其以后的结点就消失在茫茫内存中，这就关键时刻掉链子了。

所以我们要先把 new 和 previous->next（ previous 的直接后继结点）连起来，这样一来，指针 new 就保存了它所指向的及其以后的结点，

【角度二】

直接看代码，previous->next = new 执行完后 new->next = previous->next 就相当于 new->next = new ，自己指自己，这显然不正确。

总之，把核心代码理解到位，剩下的就在于如何准确的找到 previous 和 current 的位置。

2.8.2. 指定位置插入

【不带头结点】

我们需要考虑两种情况：

1. 在第一个元素前插入
2. 在其他元素前插入

/**
 * 指定插入位置
 * p_head: 指向头指针的指针
 * position: 指定位置 (1 <= position <= length + 1)
 * elem: 新结点的数据
 */ 
void insert(Node **p_head, int position, int elem)
{
    Node *new = create_node(elem);
    Node *current = *p_head;
    Node *previous = NULL;
    int length = get_length(*p_head);
    if (position < 1 || position > length + 1) {
        printf("插入位置不合法\n");
        return;
    }
    for (int i = 0; current != NULL && i < position - 1; i++) {
        previous = current;
        current = current->next;
    }
    new->next = current;
    if (previous == NULL)
        *p_head = new;
    else
        previous->next = new;
}

【带头结点】

由于带了一个头结点，所以在第一个元素前插入和在其他元素前插入时的操作是相同的。

/**
 * 指定插入位置
 * p_head: 指向头指针的指针
 * position: 指定位置 (1 <= position <= length + 1)
 * elem: 新结点的数据
 */
void insert(Node **p_head, int position, int elem)
{
    Node *new = create_node(elem);
    Node *previous = *p_head;
    Node *current = previous->next;
    int length = get_length(*p_head);
    if (position < 1 || position > length + 1) {
        printf("插入位置不合法\n");
        return;
    }
    for (int i = 0; current != NULL && i < position - 1; i++) {
        previous = current;
        current = current->next;
    }
    new->next = current;
    previous->next = new;
}

2.7.2. 头插法

【不带头结点】

不带头结点的头插法，即新插入的节点始终被头指针所指向。

/**
 * 头插法：新插入的节点始终被头指针所指向
 * p_head: 指向头指针的指针
 * elem: 新结点的数据
 */
void insert_at_head(Node **p_head, int elem)
{
    Node *new = create_node(elem);
    new->next = *p_head;
    *p_head = new;
}

【带头结点】

带头结点的头插法，即新插入的结点始终为头结点的直接后继。

/**
 * 头插法，新结点为头结点的直接后继
 * p_head: 指向头指针的指针
 * elem: 新结点的数据
 */
void insert_at_head(Node **p_head, int elem)
{
    Node *new = create_node(elem);
    new->next = (*p_head)->next;
    (*p_head)->next = new;
}

注意：多了一个头结点，所以代码有所变化。

2.7.3. 尾插法

尾插法要求我们先找到链表的最后一个结点，所以重点在于如何遍历到最后一个结点。

【不带头结点】

/**
 * 尾插法：新插入的结点始终在链表尾
 * p_head: 指向头指针的指针
 * elem: 新结点的数据
 */
void insert_at_tail(Node **p_head, int elem)
{
    Node *new = create_node(elem);
    Node *p = *p_head;
    while (p->next != NULL)   //从头遍历至链表尾
        p = p->next;
    p->next = new;
}

【带头结点】

/**
 * 尾插法：新插入的结点始终在链表尾
 * p_head: 指向头指针的指针
 * elem: 新结点的数据
 */
void insert_at_tail(Node **p_head, int elem)
{
    Node *new = create_node(elem);
    Node *p = *p_head;
    while (p->next != NULL)
        p = p->next;
    p->next = new;
}

2.8. 删除操作

2.8.0. 基本思想

删除操作是将要删除的结点从链表中剔除，和插入操作类似。

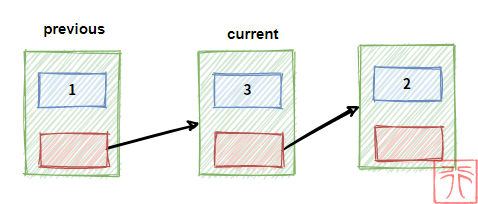
previous 和 current 为指向结点的指针，现在我们要删除结点 current，过程如下：

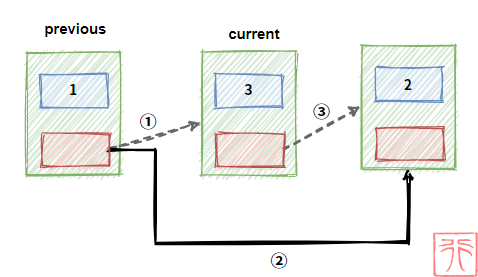
核心代码为：

previous->next = current->next;
free(current);

free() 操作将要删除的结点给释放掉。

current 指针不是必需的，没有它也可以，代码写成这样：

previous->next = previous->next->next;

但此时我们已经不能释放要删除的那个结点了，因为我们没有一个指向它的指针，它已经消失在茫茫内存中了。

2.8.2. 指定位置删除

知道了核心代码，剩下的工作就在于我们如何能够正确地遍历到要删除的那个结点。

如你所见，previous 指针是必需的，且一定是要删除的那个结点的直接前驱，所以要将 previous 指针遍历至其直接前驱结点。

【不带头结点】

/**
 * 删除指定位置的结点
 * p_head: 指向头指针的指针
 * position: 指定位置 (1 <= position <= length + 1)
 * elem: 使用该指针指向的变量接收删除的值
 */
void delete(Node **p_head, int position, int *elem)
{
    Node *previous = NULL;
    Node *current = *p_head;
    int length = get_length(*p_head);
    if (length == 0) {
        printf("空链表\n");
        return;
    }
    if (position < 1 || position > length) {
        printf("删除位置不合法\n");
        return;
    }
    for (int i = 0; current->next != NULL && i < position - 1; i++) {
        previous = current;
        current = current->next;
    }
    *elem = current->data;
    if (previous == NULL)
        *p_head = (*p_head)->next;
    else
        previous->next = current->next;
    free(current);
}

【带头结点】

/**
 * 删除指定位置的结点
 * p_head: 指向头指针的指针
 * position: 指定位置 (1 <= position <= length + 1)
 * elem: 使用该指针指向的变量接收删除的值
 */
void delete(Node **p_head, int position, int *elem)
{
    Node *previous = *p_head;
    Node *current = previous->next;
    int length = get_length(*p_head);
    if (length == 0) {
        printf("空链表\n");
        return;
    }
    if (position < 1 || position > length) {
        printf("删除位置不合法\n");
        return;
    }
    for (int i = 0; current->next != NULL && i < position - 1; i++) {
        previous = current;
        current = current->next;
    }
    *elem = current->data;
    previous->next = current->next;
    free(current);
}

通过 insert 和 delete函数，我们就能体会到不带头结点和带头结点的差别了，对于插入和删除操作，不带头结点需要额外考虑在第一个元素前插入和删除第一个元素的特殊情况，而带头结点的链表则将对所有元素的操作统一了。

还有特殊的头删法和尾删法，和头插法、尾插法并无本质区别，这里不再给出代码了

2.9. 查找和修改操作

查找本质就是遍历链表，使用一个辅助指针，将该指针正确的遍历到指定位置，就可以获取该结点了。

修改则是在查找到目标结点的基础上修改其值。

代码很简单，这里不再列出。详细代码文末获取。

2.10. 单链表的优缺点

通过以上代码，可以体会到：

优点：

• 插入和删除某个元素时，不必像顺序表那样移动大量元素。
• 链表的长度不像顺序表那样是固定的，需要的时候就创建，不需要了就删除，极其方便。

缺点：

• 单链表的查找和修改需要遍历链表，如果要查找的元素刚好是链表的最后一个，则需要遍历整个单链表，不像顺序表那样可以直接存取。

如果插入和删除操作频繁，就选择单链表；如果查找和修改操作频繁，就选择顺序表；如果元素个数变化大、难以估计，则可以使用单链表；如果元素个数变化不大、可以预估，则可以使用顺序表。

总之，单链表和线性表各有其优缺点，没必要踩一捧一。根据实际情况灵活地选择数据结构，从而更优地解决问题才是我们学习数据结构和算法的最终目的。

完整示例代码请移步至GitHub|Gitee

如有错误，还请指正。