递归和尾递归

简单的说，递归就是函数自己调用自己，它做为一种算法在程序设计语言中广泛应用。其核心思想是把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。一般来说，递归需要有边界条件、递归前进阶段和递归返回阶段。当边界条件不满足时，递归前进；当边界条件满足时，递归返回。

但是作为一个合格的程序员，我们也因该知道，递归算法相对常用的算法如普通循环等，运行效率较低。因此，应该尽量避免使用递归，除非没有更好的算法或者某种特定情况，递归更为适合的时候。在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储，递归次数过多容易造成栈溢出等。

这个时候，我们就需要用到尾递归，即一个函数中所有递归形式的调用都出现在函数的末尾，对于尾递归来说，由于只存在一个调用记录，所以永远不会发生"栈溢出"错误。

举个例子，我们来实现一下阶乘，如果用普通的递归，实现将是这样的：

function factorial(n) {
  if (n === 1) return 1;
  return n * factorial(n - 1);
}

factorial(5) // 120

最多需要保存n个调用栈，复杂度 O(n)，如果我们使用尾递归：

function factorial(n, total = 1) {
  if (n === 1) return total;
  return factorial(n - 1, n * total);
}

factorial(5) // 120

此时只需要保存一个调用栈，复杂度 O(1) 。通过这个案例，你是否已经慢慢理解其精髓了呢？接下来我将介绍几个常用的递归应用的案例，并在其后实现本文标题剖出的树的实现。

递归的常用应用案例

1. 数组求和

对于已知数组arr，求arr各项之和。

function sumArray(arr, total) {
    if(arr.length === 1) {
        return total
    }
    return sum(arr, total + arr.pop())
}

let arr = [1,2,3,4];
sumArray(arr, arr[1]) // 10

该方法给函数传递一个数组参数和初始值，也就是数组的第一项，通过迭代来实现数组求和。

2. 斐波那且数列

斐波那契数列（Fibonacci sequence），又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>=3，n∈N*）在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用。接下来我们用js实现一个求第n个斐波那契数的方法：

// 斐波那契数列
function factorial1 (n) {
    if(n <= 2){
        return 1
    }
    return factorial1(n-1) + factorial1(n-2)
}

// 尾递归优化后
function factorial2 (n, start = 1, total = 1) {
    if(n <= 2){
        return total
    }
    return factorial2 (n -1, total, total + start)
}

由尾递归优化后的函数可以知道，每一次调用函数自身，都会将更新后的初始值和最终的结果传递进去，通过回溯来求得最终的结果。

3. 阶乘

阶乘在上文以提到过，如想回顾，请向上翻阅。

4. 省市级联多级联动

省市级联多级联动的方法本质是生成结构化的数据结构，在element或antd中都有对应的实现，这里就不做过多介绍了。

5. 深拷贝

深拷贝的例子大家也已经司空见惯了，这里只给出一个简单的实现思路：

 function clone(target) {
    if (typeof target === 'object') {
        let cloneTarget = Array.isArray(target) ? [] : {};
        for (const key in target) {
            cloneTarget[key] = clone(target[key]);
        }
        return cloneTarget;
    } else {
        return target;
    }
};

6. 爬梯问题

一共有n个台阶，每次只能走一个或两个台阶，问要走完这个台阶，一共有多少种走法。

n =1; result = 1  --> 1
n =2; result = 2  --> 11 2
n =3; result = 3  --> 111 12 21
...
如果第一步走1个台阶，由以上规律可以发现剩下的台阶有n-1种走法；
如果第一步走2个台阶，由以上规律可以发现剩下的台阶有n-2种走法；
则一共有fn(n-1) + fn(n-2) 种走法
function steps(n) {
    if(n <= 1) {
        return 1
    }
    return steps(n-1) + steps(n-2)
}

7. 对象数据格式化

这道题是本人曾经面试阿里的一道笔试题，问题是如果服务器返回了嵌套的对象，对象键名大小写不确定，如果统一让键名小写。

let obj = {
    a: '1',
    b: {
        c: '2',
        D: {
            E: '3'
        }
    }
}
转化为如下：
let obj = {
    a: '1',
    b: {
        c: '2',
        d: {
            e: '3'
        }
    }
}

// 代码实现
function keysLower(obj) {
    let reg = new RegExp("([A-Z]+)", "g");
    for (let key in obj) {
        if (obj.hasOwnProperty(key)) {
            let temp = obj[key];
            if (reg.test(key.toString())) {
                // 将修改后的属性名重新赋值给temp，并在对象obj内添加一个转换后的属性
                temp = obj[key.replace(reg, function (result) {
                    return result.toLowerCase()
                })] = obj[key];
                // 将之前大写的键属性删除
                delete obj[key];
            }
            // 如果属性是对象或者数组，重新执行函数
            if (typeof temp === 'object' || Object.prototype.toString.call(temp) === '[object Array]') {
                keysLower(temp);
            }
        }
    }
    return obj;
};

具体过程和思路在代码中已经写出了注释，感兴趣可以自己研究一下。

8. 遍历目录/删除目录

我们这里使用node来实现删除一个目录，用现有的node API确实有删除目录的功能，但是目录下如果有文件或者子目录，fs.rmdir && fs.rmdirSync 是不能将其删除的，所以要先删除目录下的文件，最后再删除文件夹。

function deleteFolder(path) {
    var files = [];
    if(fs.existsSync(path)) { // 如果目录存在
        files = fs.readdirSync(path);
        files.forEach(function(file,index){
            var curPath = path + "/" + file;
            if(fs.statSync(curPath).isDirectory()) { // 如果是目录，则递归
                deleteFolder(curPath);
            } else { // 删除文件
                fs.unlinkSync(curPath);
            }
        });
        fs.rmdirSync(path);
    }
}

9. 绘制分形图形

通过递归，我们可以在图形学上有更大的自由度，但是请记住，并不是最好的选择。

我们可以借助一些工具和递归的思想，实现如上的分形图案。

10. 扁平化数组Flat

数组拍平实际上就是把一个嵌套的数组，展开成一个数组，如下案例：

let a = [1,2,3, [1,2,3, [1,2,3]]]
// 变成
let a = [1,2,3,1,2,3,1,2,3]
// 具体实现
function flat(arr = [], result = []) {
    arr.forEach(v => {
        if(Array.isArray(v)) {
            result = result.concat(flat(v, []))
        }else {
            result.push(v)
        }
    })
    return result
}

flat(a)

当然这只是笔者实现的一种方式，更多实现方式等着你去探索。

用递归画一棵自定义风格的结构树

通过上面的介绍，我想大家对递归及其应用已经有一个基本的概念，接下来我将一步步的带大家用递归画一棵结构树。 效果图：

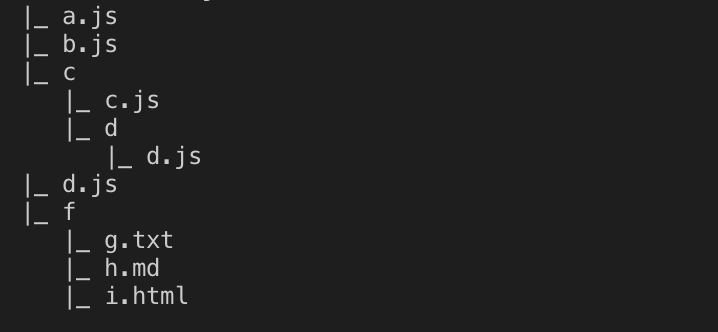
该图形是根据目录结构生成的目录树图，在很多应用场景中被广泛使用，接下来我们就来看看他的实现过程吧：

const fs = require('fs')
const path = require('path')
// 遍历目录/生成目录树
function treeFolder(path, flag = '|_') {
    var files = [];

    if(fs.existsSync(path)) {
        files = fs.readdirSync(path);
        files.forEach(function(file,index){
            var curPath = path + "/" + file;
            if(fs.statSync(curPath).isDirectory()) { // recurse
                // obj[file] = treeFolder(curPath, {});
                console.log(flag, file)
                treeFolder(curPath, '   ' + flag)
            } else {
                // obj['--'] = file
                console.log(flag, file)
            }
        })
        // return obj
    }
}

treeFolder(path.resolve(__dirname, './test'))

test为我们建的测试目录，如下：

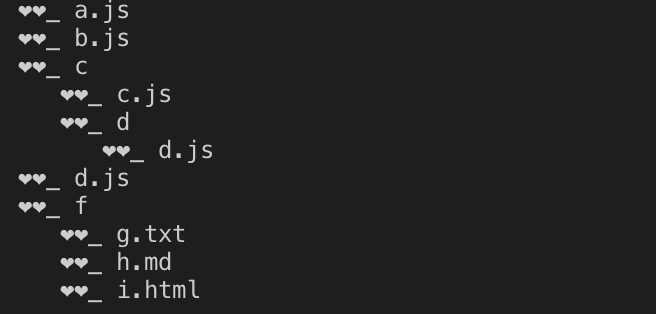
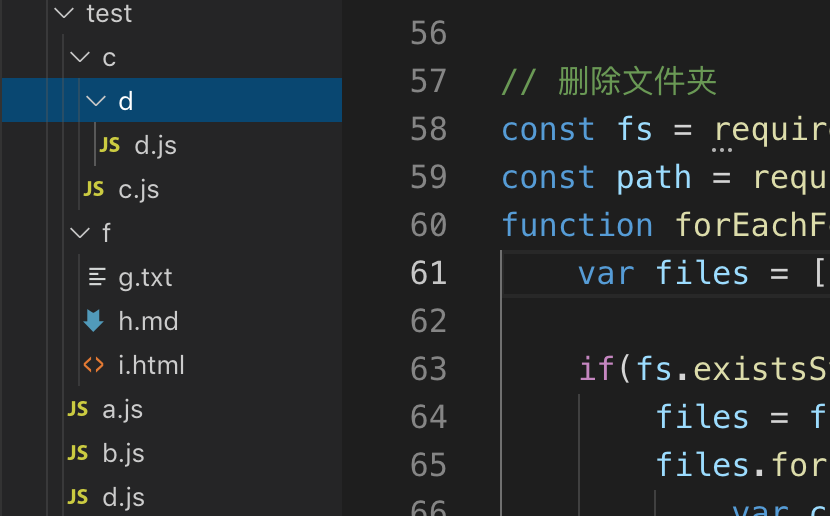我们通过短短10几行代码就实现了一个生成结构树的小应用，是不是感觉递归有点意思呢？在这个函数中，第一个参数是目录的绝对路径，第二个是标示符，标示符决定我们生成的树枝的样式，我们可以自定义不同的样式。

欢迎大家相互学习交流，一起探索前端的边界。

更多推荐

• 5分钟教你用nodeJS手写一个mock数据服务器
• 笛卡尔乘积的javascript版实现和应用
• JavaScript 中的二叉树以及二叉搜索树的实现及应用
• 用 JavaScript 和 C3 实现一个转盘小游戏
• 教你用200行代码写一个爱豆拼拼乐H5小游戏（附源码）
• 基于react/vue生态的前端集成解决方案探索与总结
• 9012教你如何使用gulp4开发项目脚手架
• 如何用不到200行代码写一款属于自己的js类库)
• 让你瞬间提高工作效率的常用js函数汇总(持续更新)
• 一张图教你快速玩转vue-cli3
• 3分钟教你用原生js实现具有进度监听的文件上传预览组件
• 3分钟教你用原生js实现具有进度监听的文件上传预览组件
• 使用Angular8和百度地图api开发《旅游清单》
• js基本搜索算法实现与170万条数据下的性能测试
• 《前端算法系列》如何让前端代码速度提高60倍
• 《前端算法系列》数组去重
• vue高级进阶系列——用typescript玩转vue和vuex
• 前端三年，谈谈最值得读的5本书籍