一、问题分析

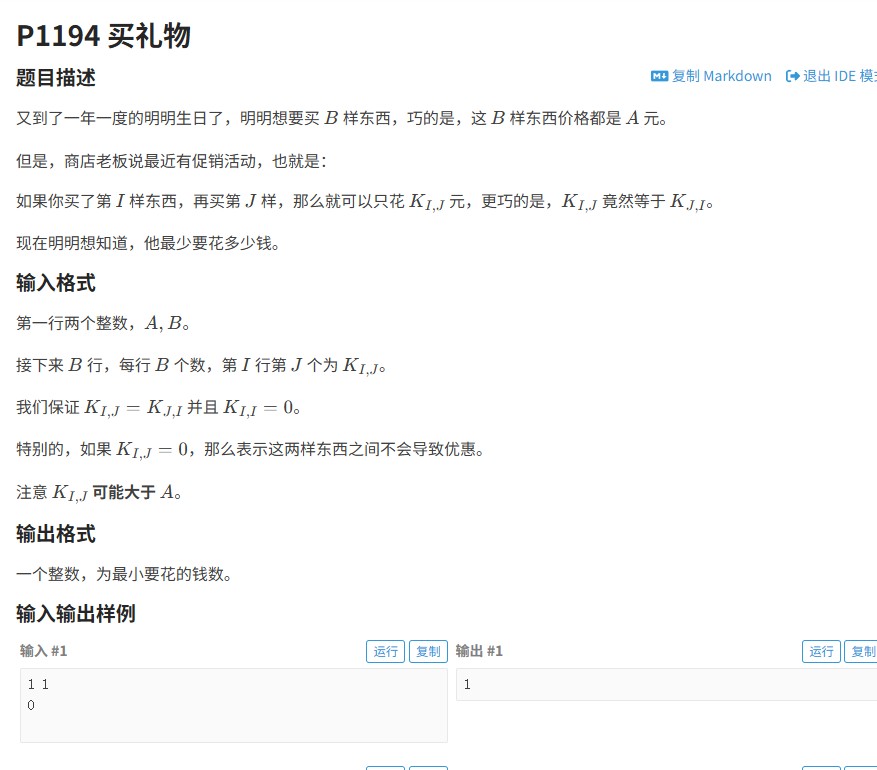
题目描述了一个促销场景：购买B件相同价格A元的商品，但购买特定组合(I,J)时可以享受优惠价K_{I,J}。我们需要计算购买所有商品的最小总花费。

二、算法选择

这个问题可以转化为图论中的最小生成树问题：

1. 将每件商品视为图中的一个节点
2. 优惠价格K_{I,J}视为节点I和J之间的边权
3. 添加一个虚拟节点0，连接到所有商品节点，边权为A

这样，原问题就转化为在这个图中找最小生成树，总权重即为最小花费。

三、C++代码实现

#include <iostream>
#include <vector>
#include <algorithm>
using namespACe std;

struct Edge {
    int u, v, w;
    bool operator<(const Edge& other) const {
        return w < other.w;
    }
};

vector<int> parent;

int find(int x) {
    return parent[x] == x ? x : parent[x] = find(parent[x]);
}

int main() {
    int A, B;
    cin >> A >> B;

    vector<Edge> edges;

    // 添加虚拟节点0到各商品的边
    for (int i = 1; i <= B; ++i) {
        edges.push_back({0, i, A});
    }

    // 读入优惠价格
    for (int i = 1; i <= B; ++i) {
        for (int j = 1; j <= B; ++j) {
            int k;
            cin >> k;
            if (i < j && k != 0) {  // 避免重复添加
                edges.push_back({i, j, k});
            }
        }
    }

    // Kruskal算法准备
    sort(edges.begin(), edges.end());
    parent.resize(B + 1);
    for (int i = 0; i <= B; ++i) parent[i] = i;

    int total = 0, count = 0;
    for (auto& e : edges) {
        int rootU = find(e.u);
        int rootV = find(e.v);
        if (rootU != rootV) {
            parent[rootV] = rootU;
            total += e.w;
            if (++count == B) break;  // 生成树有B条边
        }
    }

    cout << total << endl;
    return 0;
}

四、代码解析

1. 数据结构：使用Edge结构体存储边信息
2. 虚拟节点：节点0代表不适用任何优惠的原始购买方式
3. 并查集：用于高效判断环的存在
4. Kruskal算法：按边权排序后贪心选择最小边

来源：编程学习